Задача 1:
Внутри треугольника ABC взяли точку P.
Прямые BP и CP пересекают стороны треугольника в точках E
и F соответственно. Найдите площадь четырехугольника
AFPE, если S
BPF = 4,S
BPC = 8,S
CPE = 13.
Задача 2:
Найдите все значения, которые может принимать (20 + n²,20 + (n + 1)²).
Задача 3:
Решите уравнение:
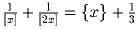
.
([x] – целая часть x, x = x – [x] – дробная часть x).
Задача 4:
В четырехугольнике ABCD стороны AB и CD параллельны, а диагонали
AC и BD перпендикулярны. Докажите, что
a) AD • BC ≥ AB • CD; b) AD + BC ≥ AB + CD.
Задача 5:
x,y,z – различные вещественные числа. Могут ли числа
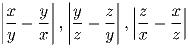
быть длинами сторон треугольника?
Задача 6:
Найдите количество неупорядоченных пар A,B подмножеств n-элементного
множества X таких, что A ≠ B и
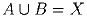
.


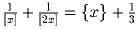 .
([x] – целая часть x, x = x – [x] – дробная часть x).
.
([x] – целая часть x, x = x – [x] – дробная часть x).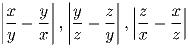
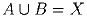 .
.