 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Олимпиада ЮМШ >> 1999 год >> Городской тур >> 5 класс | Показать решения |
|
|
| Санкт-Петербургские (Ленинградские) соревнования. Олимпиада ЮМШ. 1999 год. Городской тур. 5 класс |
|
|
Можно ли раскрасить доску размером 8 × 8 клеточек так,
чтобы в фигурке 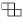 при любом ее расположении была бы ровно
одна закрашенная клетка?
при любом ее расположении была бы ровно
одна закрашенная клетка?
Задача 2:
Лев установил в лесу несколько законов: «На одной полянке не должно быть больше трех ушатых и хвостатых одновременно.», «Все волки и зайцы имеют по два уха и одному хвосту, а кроме того – острые зубы.», «Зайцы должны находиться в лесу парами.», «Зубастые звери не ходят поодиночке.», «Нельзя делать действия, заставляющие других нарушить закон.». Может ли волк на полянке съесть зайца, не нарушив законы?
Задача 3:
Паша играл в тетрис (в стакан шириной 10 клеток падают фигурки из 4 клеток; если клетки фигурок полностью заполняют какую-либо линию, она исчезает, а верхние клетки съезжают вниз). Перед выходом в школу старший брат посмотрел на экран и запомнил картинку. Придя из школы, он первым делом поинтересовался у брата: «Как игра?», на что услышал – «1999 линеек за это время уничтожил». Брат посмотрел на экран и воскликнул: «Да ведь эта та же картинка, что была перед моим уходом, только вверх ногами!». Докажите, что кто-то из них ошибся.
Задача 4:
В шахматном королевстве балетмейстер придумал «танец коней». Танцующие кони делают два «правых» шага, а потом один «левый» (шаг заключается в том, что конь скачет на 2 клетки вперед, а потом поворачивает и скачет на 1 клетку вправо, если ход «правый», или на одну клетку влево, если ход «левый»). Каковы минимально возможные размеры зала, чтобы в нем можно было танцевать этот танец?
Задача 5:У Золотой Рыбки половина всех знакомых – пескари, треть – щуки, а каждый четвертый (если смотреть по записной книжке) – карась. Сколько знакомых у Золотой Рыбки?
Задача 6:
На доске выписали все возможные девятизначные числа, которые можно получить из цифры 9, записывая каждый раз за последней цифрой либо ее же, либо цифру, меньшую ее на 1 (например, так можно получить число 998766543). Сколько раз встречается цифра 3 среди последних цифр этих чисел?
Задача 7:
Клетки двух таблиц размерами 1982 × 1983 закрашены в синий и красный цвет так, что в каждом столбце и любой строке – чётное число синих клеток. Одну из таблиц наложили на другую, при этом одна из синих клеток наложилась на красную. Докажите, что найдутся ещё три клетки, покрытые клетками противоположного цвета.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Олимпиада ЮМШ >> 1999 год >> Городской тур >> 5 класс | Показать решения |