 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Олимпиада ЮМШ >> 1999 год >> Городской тур >> 8 класс | Показать решения |
|
|
| Санкт-Петербургские (Ленинградские) соревнования. Олимпиада ЮМШ. 1999 год. Городской тур. 8 класс |
|
|
а) Кот Леопольд написал на листе бумаги цифру 9. Мыши получают девятизначные числа, записывая каждый раз за последней цифрой либо ее же, либо цифру, меньшую ее на 1 (например, так можно получить число 998766543). Сколько различных девятизначных чисел могут получить мыши?
б) Найдите, сколько раз встречается каждая цифра среди последних цифр этих чисел.
в) Найдите, сколько раз встречается цифра 7 в этих числах.
г) Леопольд нашел сумму всех этих чисел. Какой остаток она может давать при делении на 9?
Задача 2:
Хрюша нарисовал на листе ватмана четырехугольник. Потом он взял кальку и перевел на нее все стороны и все углы этого четырехугольника (каждый элемент на свой лист). Теперь Хрюша показывает своим друзьям разные листы кальки и предлагает восстановить четырехугольник. В этом сюжете все построения должны проводиться циркулем и линейкой. Во всех пунктах требуется доказательство того, что построенная фигура является искомой.
а) Постройте четырехугольник по трем углам и двум смежным сторонам. Сколько различных решений имеет эта задача?
б) Постройте четырехугольник по трем углам и двум противоположным сторонам. Сколько различных решений имеет эта задача?
в) В четырехугольнике заданы четыре стороны. Какое наименьшее количество углов надо задать для того, чтобы количество таких четырехугольников было конечно? Постройте их.
г) В четырехугольнике заданы три стороны. Какое наименьшее количество углов надо задать для того, чтобы количество таких четырехугольников было конечно? Постройте их.
Задача 3:
а) Есть два натуральных числа, сумма которых равна 120. Всегда ли числа 1,2,3,...,15 можно распределить на две группы так, чтобы сумма чисел в первой группе равнялась бы первому числу, а во второй – второму?
б) Есть три различных натуральных числа, сумма которых равна 21. Всегда ли числа 1,2,3,...,6 можно распределить по 3 группам так, чтобы сумма чисел в первой группе равнялась бы первому числу, во второй – второму, и в третьей – третьему?
в) Изменится ли ответ, если среди исходных чисел могут быть равные?
г) Пусть a, b и c – различные натуральные числа, сумма
которых равна 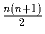 . Всегда ли числа 1,2,3,..., n можно
разбить на группы так, чтобы сумма чисел в первой группе равнялась a,
во второй – b, в третьей – c?
. Всегда ли числа 1,2,3,..., n можно
разбить на группы так, чтобы сумма чисел в первой группе равнялась a,
во второй – b, в третьей – c?
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Олимпиада ЮМШ >> 1999 год >> Городской тур >> 8 класс | Показать решения |