Задача 1: На территории завода четыре асфальтовые дорожки длиной 10 м каждая образуют квадрат. В двух соседних вершинах квадрата стоят двое рабочих, держа на плечах десятиметровую трубу. Им необходимо, передвигаясь по дорожкам и не выпуская при этом трубы, поменяться местами. Из соображений безопасности разрешается идти со скоростью не больше 1 м/с. За какое наименьшее время рабочие могут справиться с заданием? (Внутри квадрата нет никаких сооружений, создающих помехи при переноске трубы).

(И. Акулич, г. Минск)

Задача 2: Окружность пересекает стороны равностороннего треугольника в шести точках, как показано на рисунке. Докажите, что AB₂ + CA₂ + BC₂ = AC₁ + BA₁ + CB₁.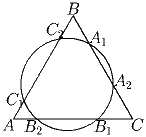

(В. Произволов)

Задача 3: Докажите, что ни при каких целых a, b и c числа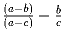 ; ; 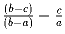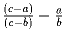. не могут быть целыми одновременно.

(В. Каскевич, г. Минск)

Задача 4: Разрежьте квадрат на шесть частей так, чтобы ими можно было полностью и без перекрытий оклеить поверхность некоторого куба.

(С. Токарев)

Задача 5: Натуральное число назовем удобным, если его можно представить в виде суммы двух натуральных слагаемых, суммы цифр которых одинаковы. Докажите, что существуют 1000000 последовательных натуральных чисел, являющихся удобными.

Задача 6: Рассмотрим множество всех квадратных таблиц p × p клеток (p > 1), заполненных натуральными числами 1,2,...,p². Пусть A – подмножество, в котором каждую таблицу можно получить из правильной операциями перестановки столбцов и перестановки строк (правильная таблица – таблица, в которой в первой строке (столбце) стоят по порядку числа 1,2, … ,p, во второй строке (столбце) – p + 1,p + 2, … ,2p, и так далее); B – подмножество, в котором из любой таблицы можно получить таблицу с равными числами операциями прибавления числа 1 ко всем числам строки или столбца. Докажите, что A = B тогда и только тогда, когда p – простое.

Задача 7: В середине одной из стен квадратной комнаты 3 × 3 имеется проход шириной 1 (рисунок 1). Можно ли в эту комнату внести какой-нибудь стол, имеющий площадь более 4?

Задача 8: Пусть [a,b,c] – наименьшее общее кратное натуральных чисел a, b и c. Может ли для каких-нибудь x, y и z оказаться, что [x,y,z] = [x + 1,y + 1,z + 1] = [x + 2,y + 2,z + 2]?