 |
 |
|
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1989 | Убрать решения |
|
|
| Турнир имени Ломоносова. Конкурс по математике. 1989 |
|
|
Будем решать задачу с конца. Определим сначала, сколько тремпончиков было у Джона перед встречей с последней девушкой. Из условия следует, что пол-тремпончика составляли половину этого количества. Значит, всего имелся один тремпончик. Аналогично, перед встречей с Банной половину всех имевшихся тремпончиков составлял этот один и еще пол-тремпончика, то есть полтора. Поэтому всего имелось три тремпончика. Они и еще пол-тремпончика составляли половину исходного количества. Значит, изначально было 7 тремпончиков.
Задача 2: (5–9) На турнире им. Ломоносова 19лохматого года в институте МИМИНО были конкурсы по математике, физике, химии, биологии и бальным танцам. Когда турнир закончился, выяснилось, что на каждом конкурсе побывало нечетное количество школьников, и каждый школьник участвовал в нечетном количестве конкурсов. Четное или нечетное число школьников пришло на турнир в МИМИНО? Решение: Напомним, что по правилам турнира им. Ломоносова каждый школьник имеет право участвовать в любом количестве конкурсов турнира.
Заметим, что сумма четного числа нечетных чисел всегда является четным числом, а сумма нечетного числа нечетных чисел всегда является нечетным числом (см. Т6).
Рассмотрим сумму количеств участников по всем пяти конкурсам. Эта сумма должна быть нечетной, так как по условию на каждом конкурсе побывало нечетное количество школьников. С другой стороны, это же число можно получить, сложив для каждого школьника количество конкурсов, в которых он участвовал. Предположим, что количество школьников было четным. Тогда рассматриваемая сумма содержит четное число нечетных слагаемых и, тем самым, является четной. Полученное противоречие показывает, что предположение было ложным. Значит, на турнир в МИМИНО пришло нечетное количество школьников.
Задача 3: (5–7) Один из пяти братьев испек маме пирог. Андрей сказал: «Это Витя или Толя". Витя сказал: «Это сделал не я и не Юра". Толя сказал: «Вы оба шутите". Дима сказал: «Нет, один из них сказал правду, а другой — нет". Юра сказал: «Нет Дима, ты не прав". Мама знает, что трое из ее сыновей всегда говорят правду. Кто испек пирог? Решение: Рассмотрим отдельно три возможных случая.
1) Андрей и Витя оба лгут. Это значит, что Толя говорит правду, Дима лжет, Юра говорит правду.
2) Один из ребят (Андрей или Витя) говорит правду, а второй лжет. В этом случае Толя лжет, Дима говорит правду, Юра лжет.
3) Андрей и Витя оба говорят правду. Тогда Толя и Дима лгут, Юра говорит правду.
Лишь в третьем случае правду говорят трое из братьев. Значит, только этот случай мог иметь место. Поскольку Андрей говорит правду, то пирог испек либо Витя, либо Толя. Однако Витя (а он, как мы выяснили, тоже говорит правду) отрицает, что он это сделал. Значит, пирог испек Толя. При этом Андрей, Витя и Юра сказали правду.
Задача 4: (5–7) Даны две окружности и точка. Построить отрезок, концы которого лежат на данных окружностях, а середина — в данной точке. Решение: При центральной симметрии относительно середины отрезка один его конец переходит в другой. На этом очевидном замечании и базируется требуемое построение. Отобразим одну из данных окружностей симметрично относительно данной точки (рис. 31). Точка пересечения образа этой окружности со второй окружностью и будет концом искомого отрезка. Отразив один конец относительно середины, находим второй конец.
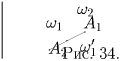
Задача может не иметь решений или иметь одно, два или бесконечно много решений в зависимости от количества точек пересечения образа первой окружности со второй окружностью (бесконечно много решений будет в случае, если данные окружности симметричны относительно данной точки).
Задача 5: (8–9) На конкурсе по математике в институте МИМИНО предлагалось 20 задач. На закрытие пришло 20 школьников. Каждый из них решил по две задачи, причем выяснилось, что среди пришедших каждую задачу решило ровно два школьника. Докажите, что можно так организовать разбор задач, чтобы каждый школьник рассказал одну из решенных им задач, и все задачи были разобраны. Решение: Организуем разбор следующим образом. В каждый момент определим кандидатами на рассказ решения следующей задачи всех школьников, еще не рассказывавших решение, но решивших одну из уже разобранных задач. Если таких кандидатов нет, то просим любого школьника, еще не рассказывавшего решения, разобрать любую из решенных им задач. Если же хотя бы один кандидат существует, то просим его разобрать еще не разобранную решенную им задачу. При таком способе разбора в любой момент может быть не более одного кандидата, и, если кандидат существует, то одна из решенных им задач еще не разбиралась.
Заметим, что фактически приведенное решение повторяет (хотя и в других терминах) доказательство факта, что граф, из каждой вершины которого выходит ровно два ребра, является объединением циклических (см. Т14).
Задача 6: (8–9) По окончании конкурса бальных танцев, в котором участвовали 7 мальчиков и 8 девочек, каждый (каждая) назвал (назвала) количество своих партнерш (партнеров): 3, 3, 3, 3, 3, 5, 6, 6, 6, 6, 6, 6, 6, 6, 6. Не ошибся ли кто-нибудь из них? Решение: Сумма чисел, названных всеми мальчиками, должна равняться сумме чисел, названных всеми девочками. Действительно, обе эти суммы должны равняться количеству пар, образовавшихся во время конкурса. Поскольку сумма всех названных чисел равна 74, то каждая из сумм чисел, названных мальчиками и девочками в отдельности, должна равняться 37. Однако, из названных чисел невозможно выбрать часть, дающую в сумме 37. Действительно, все названные числа кроме пятерки делятся на 3. Поэтому любой набор этих чисел, не содержащий пятерки, дает в сумме число, делящееся на 3. Сумма чисел любого набора, содержащего пятерку, дает при делении на 3 остаток 2. Число 37 при делении на 3 дает остаток 1, поэтому сумма чисел такого набора не может равняться 37.
Задача 7: (8–9) Одно из чисел получается из другого перестановкой цифр. Может ли их сумма равняться 999…9 (999 девяток)? Решение:
Предположим, что такая пара чисел существует. Очевидно, что десятичная запись каждого из этих чисел содержит 999 цифр. Поскольку их сумма записывается одними девятками, одно получается из другого заменой каждой цифры ее дополнением до девятки (то есть каждая цифра a заменяется на цифру 9 – a). Предположим, это дополнение состоит из тех же цифр, что и исходное число. Так как записи чисел состоят из одних и тех же чисел, то количество нулей должно в этих записях равняться количеству девяток, количество единиц — количеству восьмерок, количество двоек — количеству семерок, количество троек — количеству шестерок и количество четверок — количеству пятерок. Но это возможно лишь в случае, если количество цифр в записи числа четно. Противоречие доказывает, что пары чисел с указанными свойствами быть не может.
Задача 8: (8–9) Восстановите а) треугольник; б) пятиугольник по серединам его сторон. Решение:
а) Пусть ABC — искомый треугольник, A′,
B′, C′ — данные точки, середины его сторон BC,
CA и AB соответственно (рис. 32). Тогда, согласно свойству
средней линии треугольника, 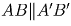 ,
,
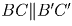 ,
, 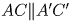 .
.
Построение будем производить следующим образом. Через точку A проведем прямую a, параллельную B′C′, через точку B′ — прямую b, параллельную A′C′, через точку C′ — прямую c, параллельную A′B′. Треугольник ABC, ограниченный прямыми a, b и c, будет искомым.
Докажем это. Четырехугольник 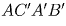 является
параллелограммом. Поэтому
является
параллелограммом. Поэтому 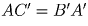 .
Четырехугольник
.
Четырехугольник 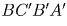 также является
параллелограммом. Поэтому
также является
параллелограммом. Поэтому 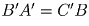 .
Значит,
.
Значит, 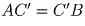 , т.е.
, т.е. 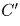 — середина
стороны AB. Аналогично доказывается, что
— середина
стороны AB. Аналогично доказывается, что 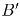 — середина AC,
а
— середина AC,
а  — середина BC.
— середина BC.
Задача имеет единственное решение во всех случаях, когда данные три точки не лежат на одной прямой.
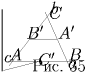

б) Пусть ABCDE — искомый пятиугольник, A′,
B′, C′, D′ и E′ — данные точки, середины его сторон CD,
DE и EA, AB и BC соответственно (рис. 36).
Опять воспользуемся свойством средней линии треугольника, записав
его в векторном виде. Применим его к треугольникам ABC, BCD,
CDE, DEA и EAB. Имеем
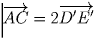 ,
,
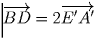 ,
,
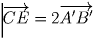 ,
,
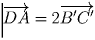 ,
,
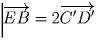 .
.
Из проведенного анализа вытекает следующий способ построения.
Выбираем произвольную точку A1. Далее находим
точки C1, E1, B1 и D1, откладывая последовательно
векторы
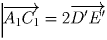 ,
,
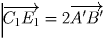 ,
,
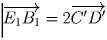 ,
,
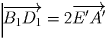 .
Искомый пятиугольник ABCDE получается из пятиугольника
A′B′C′D′E′ параллельным переносом. Вектор переноса можно взять с
началом в середине стороны A′B′ и концом в точке D.
.
Искомый пятиугольник ABCDE получается из пятиугольника
A′B′C′D′E′ параллельным переносом. Вектор переноса можно взять с
началом в середине стороны A′B′ и концом в точке D.
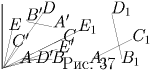
Задача имеет единственное решение, если полученные точки A1, B1, C1, D1 и E1 являются последовательными вершинами пятиугольника (другими словами, замкнутая ломаная A1B1C1D1E1A1 не самопересекающаяся).
Задача 9: (8–9) Первоклассник Петя знает только цифру 1. Докажите, что он может написать число, делящееся на 1989. Решение:
Рассмотрим последовательность a1 = 1, a2 = 11, …, an = 11 … 1, …чисел, десятичная запись которых состоит из одних единиц. Поскольку существует лишь конечное число различных остатков от деления на 1989, а последовательность содержит бесконечно много членов, то, согласно принципу Дирихле (см. Т2), среди них найдутся два, дающих одинаковые остатки при делении на 1989. Пусть это числа ak и al, (k > l). Тогда их разность ak – al = 10lak – l делится на 1989 (см. Т5). Так как 10l и 1989 — взаимно просты, то ak – l делится на 1989 (см. Т4). Это число Петя сможет записать.
Задача 10: (8–9) Каков наибольший возможный общий делитель чисел 9m + 7n и 3m + 2n, если числа m и n не имеют общих делителей, кроме единицы?
Решение: Любой общий делитель чисел x = 9m + 7n и y = 3m + 2n должен быть также делителем чисел x – 3y = n и 7y – 2x = 3m. Поскольку числа m и n не имеют общих делителей кроме 1, то любой общий делитель чисел n и 3m должен быть делителем числа 3 (см. Т4). Поэтому он не может быть больше трех.
Покажем, что равняться трем он может. Пусть m = 1, n = 3. Тогда x = 30, y = 9. Число 3 является общим делителем чисел 30 и 9.
Задача 11: (8–9) Барон Мюнхгаузен заявил Георгу Кантору, что он может выписать в ряд все натуральные числа без единицы так, что только конечное их число будет больше своего номера. Не хвастает ли барон?Решение: Пусть a1,a2, … ,an, … — выписанные в ряд все натуральные числа без единицы. Покажем, что в этой последовательности существует бесконечно много чисел, больших своего номера. Построим для этого новую последовательность bn натуральных чисел, заданную следующим рекуррентным (см. Т1) соотношением:
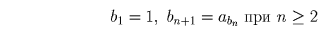
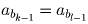 , откуда
bk – 1 = bl – 1, так как все члены последовательности an
различны. Продолжая аналогичные рассуждения, получим
bk – 2 = bl – 2
…
bk – l + 1 = b1
Последнее равенство означает
, откуда
bk – 1 = bl – 1, так как все члены последовательности an
различны. Продолжая аналогичные рассуждения, получим
bk – 2 = bl – 2
…
bk – l + 1 = b1
Последнее равенство означает 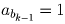 ,
что противоречит условию того, что последовательность an не
содержит единицы. Противоречие доказывает, что все члены
последовательности bn различны.
,
что противоречит условию того, что последовательность an не
содержит единицы. Противоречие доказывает, что все члены
последовательности bn различны.Так как bn — бесконечная последовательность различных
натуральных чисел, то в ней существует бесконечно много членов,
больших предыдущего (в противном случае она бы убывала начиная с
некоторого места, что невозможно). Иными словами, для бесконечно
многих k выполнено bk + 1 > bk, или 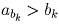 . А это и
значит, что бесконечно много членов последовательности an
больше своего номера.
. А это и
значит, что бесконечно много членов последовательности an
больше своего номера.
Задача 12: (8–9) Три окружности попарно пересекаются. Для каждой пары окружностей через точки их пересечения проведена прямая. Докажите, что эти три прямые либо попарно параллельны, либо пересекаются в одной точке.
Решение: Каждая из проведенных прямых является множеством точек, степени которых относительно двух из данных окружностей равны (см. Т20). Поэтому если какие-то две из трех проведенных прямых пересекаются, то точка их пересечения имеет одинаковую степень относительно всех трех окружностей. Значит, третья прямая также проходит через эту точку.
Приведем кратко другой способ решения задачи, опирающийся на «выход в пространство". Построим три сферы, для которых данные окружности являются большими окружностями (то есть с теми же центрами и радиусами.) Пересечением любой пары этих окружностей является окружность, проектирующаяся в отрезок, соединяющий точки пересечения соответствующих окружностей. Точка пересечения сфер проектируется в точку пересечения этих отрезков.
Задача 13: (6–8) Найдите все простые числа, которые нельзя записать в виде суммы двух составных. Решение:
Докажем, что любое простое число p, большее 11, представляется в виде суммы двух составных. Поскольку любое простое число, большее двух, нечетно, то число p — нечетное, а p – 9 — четное и, следовательно, составное. Поэтому p = (p – 9) + 9 — искомое представление.
С другой стороны, непосредственно проверяется, что все простые числа, меньшие или равные 11 (а это — 2, 3, 5, 7 и 11), не представимы в виде суммы двух составных.
Задача 14: (6–8) Решить уравнение в целых положительных числах
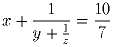
Любое число единственным образом представляется в виде суммы двух
чисел, одно из которых — целое, а другое — неотрицательно и
меньше единицы. Это — сумма его целой и дробной части. Для
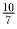 таким представлением будет
таким представлением будет
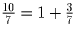 . Поэтому x = 1,
. Поэтому x = 1, 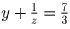 . Аналогично разлагаем
. Аналогично разлагаем 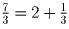 в
сумму целой и дробной части. Получаем y = 2, z = 3.
в
сумму целой и дробной части. Получаем y = 2, z = 3.
Задача 15: (8) Пусть a, b, c — длины сторон треугольника; α , β , γ — величины противолежащих углов. Докажите, что a α + b β + c γ ≥ a β + b γ + c α .
Решение:
Воспользуемся тем, что в треугольнике против большего угла лежит большая сторона (см. Т19). Поскольку приведенное неравенство не изменяется при циклической перестановке сторон a, b и c (и, соответственно, углов α , β и γ ), можно без ограничения общности считать, что c — наименьшая сторона треугольника (соответственно, γ — наименьший угол). Рассмотрим теперь разность правой и левой частей доказываемого неравенства. a α + b β + c γ – a β – b γ – c α = (b – c)( α – γ ) + (a – b)( α – γ ). Первое слагаемое правой части есть произведение двух неотрицательных (в силу сделанного предположения) чисел, второе — двух чисел одного знака, поскольку условия A ≥ B и α ≥ β равносильны (в силу упомянутого выше свойства треугольника). Итак, рассматриваемая разность неотрицательна, отсюда следует справедливость неравенства.
Фактически, утверждение задачи вытекает из следующего более общего факта. Пусть a1 < a2 < … < an и b1 < b2 < … < bn — два упорядоченных одинаковой длины набора чисел. Тогда максимальная сумма попарных произведений чисел этих наборов — это a1b1 + a2b2 + … + anbn, а минимальная — a1bn + a2bn – 1 + … + anb1. Попробуйте доказать его самостоятельно. Указание: исследуйте, что происходит с такой суммой при перестановке некоторых bi и bj.
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1989 | Убрать решения |