Задача 1:
Найти все целые x, для которых
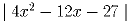
–
простое число.
Решение:
|4x² – 12x – 27| = |2x – 9| • |2x + 3|, значит,
один из множителей равен единице, а другой простому
числу. Приравнивая каждый из сомножителей единице, получаем ответы:
– 2; – 1; 4; 5.
Задача 2:
a > b > 0; a² + b² = 6ab. Найти
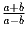
.
Решение: 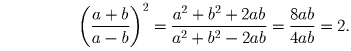
Поскольку a > b > 0, то
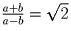
.
Задача 3:
Из точки M, взятой вне угла A, проведены к нему две секущие
прямые, одна из которых отсекает на сторонах угла два равных
отрезка AB и AC, а другая пересекает эти стороны в точках D и E
соответственно. Доказать, что BD:CE = MD:ME.
Решение:
Проведём DK || AE (K – лежит на прямой BM)
треугольник KDB подобен треугольнику CAB и, следовательно, также
равнобедренный (BD = KD). Из подобия треугольников CEM и KDM
следует равенство
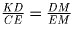
,
откуда
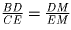
, из которого заменой KD на
BD получаем искомое.
Задача 4:
x
x + y
y = x
y + y
x, x и y – натуральные числа.
Докажите, что x = y.
Решение:
Переписав равенство в виде
x
y(x
x – y – 1) = y
y(y
x – y – 1), заметим, что x ≤ y. Аналогично, вынося за скобки y
x, убедимся, что y ≤ x. Значит, x = y.
Задача 5:


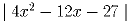 –
простое число.
–
простое число.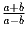 .
.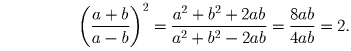
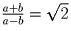 .
Задача 3:
Из точки M, взятой вне угла A, проведены к нему две секущие
прямые, одна из которых отсекает на сторонах угла два равных
отрезка AB и AC, а другая пересекает эти стороны в точках D и E
соответственно. Доказать, что BD:CE = MD:ME.
.
Задача 3:
Из точки M, взятой вне угла A, проведены к нему две секущие
прямые, одна из которых отсекает на сторонах угла два равных
отрезка AB и AC, а другая пересекает эти стороны в точках D и E
соответственно. Доказать, что BD:CE = MD:ME.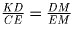 ,
откуда
,
откуда 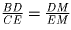 , из которого заменой KD на
BD получаем искомое.
, из которого заменой KD на
BD получаем искомое.