Задача 1: Найдите все такие четверки натуральных чисел, x,y,z,t, которые образуют арифметическую прогрессию и такие, что x³ + y³ + z³ = t³.

Решение: Пусть d – разность искомой арифметической прогрессии. Тогда y = x + d,z = x + 2d,t = x + 3d и по условию x³ + (x + d)³ + (x + 2d)³ = (x + 3d)³. Следовательно, x³ + (x + d)³ = (x + 3d)³ – (x + 2d)³ и раскладывая обе части этого соотношения по известным формулам, имеем (x + x + d)(x² – x(x + d) + (x + d)²) = (x + 3d – (x + 2d))((x + 2d)² + \  + (x + 2d)(x + 3d) + (x + 3d)²). 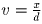Разделим обе части этого однородного относительно x и d уравнения на d³ и после приведения подобных в обеих частях получим для переменной следующее уравнение 2v³ + 3v² + 3v + 1 = 3v² + 15v + 19. Отсюда следует, что v³ – 6v – 9 = 0. Добавим и вычтем 3v в этом уравнении. Тогда v³ – 9v + 3v – 9 = v(v² – 9) + 3(v – 3) = (v – 3)(v(v + 3) + 3) = 0. Так как квадратное уравнение v(v + 3) + 3 = 0 не имеет действительных корней, то v = 3. Значит, x = 3d,y = 4d,z = 5d,t = 6d, где d – любое натуральное число.

Задача 2:

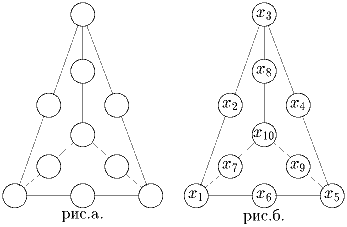
Можно ли расставить числа от 0 до 9 в кружочках (см. рисунок) так, чтобы сумма трех чисел по любому из отрезков была одной и той же?

(Рекомендована жюри Российской олимпиады.)

Решение: Расставим числа так как на рисунке 15.б. По условию 6n = 3(x₁ + x₃ + x₅ + x₁₀) + x₂ + x₄ + x₆ + x₇ + x₈ + x₉, где n – сумма чисел по каждому из отрезков. Но тогда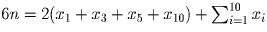 . Поэтому 6n = 2(x₁ + x₃ + x₅ + x₁₀) + 45. Противоречие.

Задача 3:

Дана полоска клетчатой бумаги длиной в 100 клеток. Двое играющих по очереди красят клетки в чёрный цвет, причём первый всегда красит 4 подряд стоящие клетки, а второй – три подряд стоящие. Уже покрашенную клетку вторично раскрашивать нельзя. Проигрывает тот, кто не может сделать очередной ход. Кто выиграет при наилучшей игре с обеих сторон?

(Рекомендована жюри Российской олимпиады.)

Решение: Выигрышная стратегия второго игрока: первым своим ходом он отступает от одного из краёв на 3 клетки (назовём их резервом) и красит три следующие. В дальнейшем он играет как угодно, не трогая резерва. Когда все такие ходы иссякнут, у первого также не будет возможности хода, и тогда второй закрашивает резерв и выигрывает.

Задача 4:

На прямой заданы последовательно точки B,L,C,F так, что 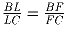. Через точки L и F проведена окружность так, что LF – диаметр. Пусть A произвольная точка окружности, не лежащая на прямой. Доказать, что AL – биссектриса угла  ∠ BAC.

(Предложена В.Н.Ушаковым.)

Решение:

первый способ. Выберем точку A на верхней полуокружности и соединим A и L (см. рисунок). Через точку C проведем прямую параллельную AL. Пусть C′ – точка пересечения этой прямой с прямой AB. На прямой BF отложим вправо от F отрезок 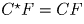и соединим c C′.

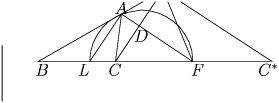
Рассмотрим теперь треугольник  ∆ C′BC. Он по построению подобен  ∆ ABL и, значит, 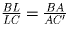. С другой стороны, имеем 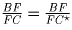по построению точки 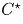. Из вышеприведенных равенств мы имеем равенство 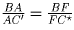. Отсюда следует, что 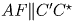. Учитывая также, что AL\|C′C, получаем подобие треугольников  ∆ ALF и 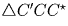. Поскольку  ∆ ALF – прямоугольный треугольник с прямым углом  ∠ A, то 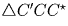 – также прямоугольный треугольник с прямым углом  ∠ C′. Но тогда отрезок 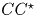можно рассматривать как диаметр окружности, в которую вписан треугольник 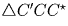, причем F – центр этой окружности (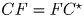). Но тогда C′F = CF, то есть треугольник  ∆ C′CF равнобедренный. Поскольку угол  ∠ D при пересечении C′C и AF – прямой, то DF – высота в равнобедренном треугольнике  ∆ C′FC, и, значит, медиана. Но тогда C′D = CD, и, следовательно, прямоугольные треугольники  ∆ ADC′ и  ∆ ADC равны. Значит,  ∠ AC′D =  ∠ ACD. С другой стороны,  ∠ BAL =  ∠ AC′D, как соответственные углы, а  ∠ LAC =  ∠ ACD, как накрест лежащие. Из последних равенств получаем  ∠ BAL =  ∠ LAC, то есть AL – биссектриса угла  ∠ BAC, что и требовалось доказать.

второй способ. Пусть O – середина отрезка LF Направим ось OX вдоль прямой BL, и примем радиус окружности за единицу масштаба. Тогда координаты точек L и F – ( – 1;0) и (1;0) соответственно. Пусть ( – b) – абсцисса точки B (без ограничения общности b > 0). Тогда x – абсцисса точки C находится из уравнения 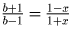. Она равна 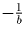. Возьмём произвольную точку окружности A. Можно считать, что ордината A положительна, поэтому 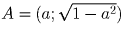. 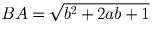Тогда , и 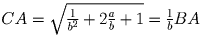, откуда 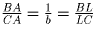, то есть AL действительно биссектриса угла BAC.