Задача 1: Можно ли расположить по кругу 2¹⁹⁹⁵ букв А и Б так, чтобы любое слово длины 1995 можно было прочитать, двигаясь по ходу часовой стрелки (без пропусков)?

Задача 2: Докажите конечность множества натуральных чисел n, делящихся нацело на все натуральные числа, не превосходящие .

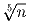Решение: Предположим, существует такое число n > 100⁵. Пусть 2^a – наибольшая степень двойки, не превосходящая 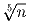; 3^b,5^c,7^d,11^e,13^f,17^g,19^h,23ⁱ,29^j – наибольшие степени соответствующих простых чисел, не превосходящие 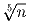. Число n должно делиться на каждую из этих степеней, а значит, и на их произведение. Но из того, что эти степени наибольшие, следует, что 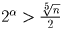, …, 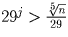. Но, значит, произведение этих степеней превышает 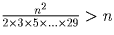. Однако, число n не может делиться на число, большее n. Следовательно, все числа рассматриваемого множества не превосходят 100⁵.

Задача 3: Внутри треугольника ABC взята точка M. Докажите неравенство:

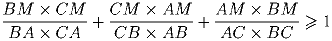
Задача 4: Многочлен P(x) = xⁿ + x^n – 1 +  …  + x + 1 разложен в произведение двух многочленов, коэффициенты при старших степенях которых равны 1, а все остальные коэффициенты неотрицательны. Докажите, что все коэффициенты этих многочленов равны 0 или 1.

Задача 5: При каких n ≥ 4 существует выпуклый n-угольник, каждая диагональ которого перпендикулярна некоторой его стороне?

Задача 6: Уравнение x³ + ax² + bx + c = 0 имеет три различных действительных корня. Докажите, что разность между наибольшим и наименьшим из его корней не меньше .

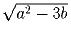Решение: Пусть x₁ > x₂ > x₃ – эти корни. По теореме Виета получаем, что нам нужно доказать, что

После преобразований получаем: (x₁ – x₂)(x₂ – x₃), т.е. верное неравенство.

Задача 7: Сфера окрашена в два цвета. Докажите, что найдутся три точки одного цвета, являющиеся вершинами правильного треугольника.

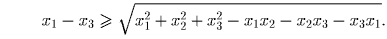
Решение: Предположим противное. Нетрудно убедиться, что найдутся две диаметрально противоположные точки одного цвета. Впишем в сферу икосаэдр так, чтобы эти две точки совпали с какими-то двумя из его вершин. Рассматривая цвета вершин икосаэдра, легко получаем утверждение задачи.

Задача 8: Дано 1995 множеств, причем каждое из них содержит 45 элементов и любые два имеют ровно один общий элемент. Докажите, что все эти множества имеют общий элемент.

Решение: Рассмотрим любое множество A. По принципу Дирихле оно содержит элемент x, входящий не менее чем в 45 других множеств 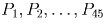. Но тогда множества P_j попарно не пересекаются ни по каким другим элементам, кроме x. Предположим, существует множество B, не содержащее элемент x. Оно пересекается с каждым из P_j, причем все элементы пересечений различны. Но тогда оно уже состоит из 45 элементов и не сможет пересечься с множеством A. Противоречие.

Задача 9: На доске в строчку написаны 12 звездочек. Два игрока по очереди заменяют любую звездочку произвольной ненулевой цифрой. Второй игрок выигрывает, если число, получившееся после 12 ходов, делится на 13, и проигрывает в противном случае. Кто выигрывает при правильной игре?

Решение: Выигрывает второй, т.к. он может добиться того, чтобы число делилось на 1001 – для этого достаточно разбить все 12 мест на пары.

Задача 10: Дан остроугольный треугольник ABC. Биссектриса угла A пересекает сторону BC в точке L, а описанную окружность треугольника ABC – в точке N. Точки K и M – основания перпендикуляров, опущенных из L на AB и AC соответственно. Докажите, что площадь четырехугольника AKNM равна площади треугольника ABC.