 |
 |
|
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Неравенство треугольника | Показать решения |
|
|
| Математический кружок. Задачник первого-второго года обучения. Неравенство треугольника |
|
|
a) Доказать, что в четырехугольнике любая сторона меньше суммы остальных.
b) То же для любого многоугольника.
Задача 4: Есть 7 прутьев длиннее 9 см, но короче 1 м. Доказать, что из трех из них можно составить треугольник.
Задача 5: Найти точку на данной прямой, сумма расстояний от которой до двух данных точек минимальна. Задача 6: Найти точку внутри четырехугольнике, сумма расстояний от которой до вершин минимальна. Задача 7: A и B – точки внутри многоугольника. Доказать, что расстояние между ними меньше половины периметра многоугольника.
Задача 8: Доказать, что в выпуклом четырехугольнике сумма диагоналей больше суммы противоположных сторон.
Задача 9: Доказать, что в выпуклом четырехугольнике сумма диагоналей больше полупериметра, но меньше периметра.
Задача 10: Доказать, что в выпуклом n-угольнике (n > 3) не больше двух сторон, которые длиннее любой диагонали.
Задача 11: Один треугольник лежит внутри другого. Доказать, что периметр внутреннего треугольника меньше периметра внешнего
a) если треугольники имеют общую сторону и угол.
b) если треугольники имеют общий угол.
c) если треугольники имеют общую сторону.
d) в общем случае.
Задача 12: Один выпуклый многоугольник лежит внутри другого. Доказать, что периметр у внутреннего многоугольника меньше, чем у внешнего.
Задача 13: Доказать, что перпендикуляр короче наклонной.
Задача 14: В лесу 100 деревьев. Высота любого больше 10, но меньше 40 метров. Расстояние между любыми двумя деревьями не больше разности их высот. Доказать, что лес можно обнести забором длинны 81 метр.
Задача 15: Доказать, что сумма расстояний от точки внутри треугольника до его вершин больше его полупериметра, но меньше периметра.
Задача 16: Доказать, что в выпуклом 5-угольнике сумма диагоналей больше периметра, но меньше удвоенного периметра. Задача 17: a) Доказать, что из двух наклонных короче та, которая ближе к перпендикуляру.
b) В треугольнике ABC точка L лежит на стороне BC. Доказать, что AL < max (AB,AC).
c) Доказать, что отрезок, лежащий внутри треугольника, короче его наибольшей стороны.
Задача 18: Доказать,что в треугольнике со сторонами a,b,c и медианой mb a)
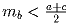 ,
b)
,
b) 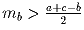 .
Задача 19:
Дан угол и точки A и B внутри него. Найти X и Y на сторонах
угла такие, что длина пути AXYB минимальна.
.
Задача 19:
Дан угол и точки A и B внутри него. Найти X и Y на сторонах
угла такие, что длина пути AXYB минимальна.Задача 20: На столе лежат несколько разных, но правильно идущих часов. Доказать, что найдется момент, когда сумма расстояний от центра стола до концов минутных стрелок больше суммы расстояний от центра стола до центров часов. Задача 21: Доказать, что в любом выпуклом 5-угольнике есть три диагонали, из которых можно составить треугольник.
Задача 22: Многоугольник, вырезанный из бумаги, сложили, перегнув по одной линии. Доказать, что в результате этого периметр уменьшился.
Задача 23: Стороны треугольника выражаются целыми числами. Может ли его медиана иметь длину 1?
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Неравенство треугольника | Показать решения |