 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 6 класс >> Принцип Дирихле-2. Сначала сосчитаем | Убрать решения |
|
|
| Разное. Материалы Кировской ЛМШ, 2000 г, 6 класс. Принцип Дирихле-2. Сначала сосчитаем |
|
|
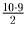 , поэтому на какую-то
пару приходится не менее двух открыток, ч.т.д.
Задача 3:
Докажите, что в любой момент однокругового чемпионата найдутся две
команды, сыгравшие одинаковое число матчей.
Решение:
Не может существовать двух команд, одна из которых не сыграла
ни одного матча, а другая – все матчи.
Задача 4:
Числа 1, 2, …, 7 разбиты на две группы. Докажите, что
произведение чисел хотя бы в одной из групп меньше 72.
, поэтому на какую-то
пару приходится не менее двух открыток, ч.т.д.
Задача 3:
Докажите, что в любой момент однокругового чемпионата найдутся две
команды, сыгравшие одинаковое число матчей.
Решение:
Не может существовать двух команд, одна из которых не сыграла
ни одного матча, а другая – все матчи.
Задача 4:
Числа 1, 2, …, 7 разбиты на две группы. Докажите, что
произведение чисел хотя бы в одной из групп меньше 72.Задача 5: Цифры 1, 2, …, 9 разбили на 3 группы. Докажите, что произведение чисел в хотя бы одной группе меньше 72. Решение: Перемножим числа в трёх группах и докажем, что 9! < 72³.
Задача 6: Докажите, что из любых 10 чисел можно выбрать несколько, сумма которых делится на 10. Решение: Эта задача содержит идею «вспомогательной последовательности сумм». Рассмотрим 10 сумм a1, a1 + a2, …a1 + a2 + … + a10. Среди них либо есть сумма, делящаяся на 10, либо две суммы с одинаковыми последними цифрами.
Задача 7: Докажите, что из 65 целых чисел всегда можно найти ровно 9 таких, сумма которых делится на 9. Решение: Рассмотрим, сколько из чисел имеют одинаковые остатки при делении на 9. Если какой-то из остатков повторяется не менее 9 раз, то берем ровно 9 чисел с этим остатком. Если же такого остатка нет, то среди 65 чисел обязательно встретятся все 9 различных остатков. Возьмем по одному «представителю» – их сумма будет кратна 9. Задача 8: Докажите, что из 65 целых чисел либо найдутся 9 таких, что каждое из чисел этой девятки, кроме последнего, делится на число, стоящее за ним, либо найдется девять таких чисел, что ни одно из них не делится на другое. Решение: Будем выписывать в строчку числа до тех пор, пока следующее делится на предыдущее. Когда встретится число, не делящееся на предыдущее, начнем им новую строчку. В дальнейшем для каждого нового числа проверяем его делимость на последние числа во всех уже выписанных строчках, и если оно делится, то вписываем его. Если же делимости ни на одно из чисел нет, то снова начинаем новую строчку. В результате таких операций получим либо табличку, в которой более 8 строк, либо табличку, в которой хотя бы одна из строк содержит более восьми чисел. Задача 9: Верно ли, что среди любых 34 разных натуральных чисел, не превосходящих 50, всегда можно выбрать два числа, одно из которых вдвое больше другого? Решение: Да, верно.
Разобьем числа на такие пары-клетки:
(1,2), (3,6), (5,10), …, (25,50);
(4,8), (12,24), (20,40);
(16,32);
Добавим к этим 17-ти парам ещё не использованные 16 чисел, не превосходящих 50 (27, 28, 29, 31, 33, 35, 36, 37, 39, 41, 43, 44, 45, 47, 48, 49), каждое из них образует отдельную клетку. Всего получилось 33 клетки, поэтому в одну из них попадут хотя бы два данных числа. В «одноместную» клетку они попасть не могут, значит они попали в пару, так что одно из них действительно в два раза больше другого.
Задача 10: Докажите, что из 26 различных натуральных чисел, не превосходящих 50, всегда можно выбрать два числа, одно из которых делится на другое. Решение: Разобьем числа на «цепочки»:1-2-4-8-16-32;
3-6-12-24-48;
5-10-20-40;
…
25-50;
27;
…
49
Иначе говоря, каждая цепочка однозначно задана своим наименьшим нечётным делителем. Цепочек всего 25, поэтому какие-то два из 26 чисел попадут в одну и ту же цепочку.
Задача 11: Попробуйте обобщить предыдущую задачу, если вместо 50 в условии будет стоять произвольное чётное число 2N. (Какое число должно стоять вместо числа 26?) Решение: N + 1Задача 12: Дано 20 различных натуральных чисел, меньших 70. Рассматриваются всевозможные их попарные разности (из большего числа вычитают меньшее). Докажите, что среди них всегда найдутся четыре одинаковых. Решение: Простая оценка числа попарных разностей не дает требуемого результата. Правильная оценка строится так: будем считать, что числа упорядочены по возрастанию, и рассмотрим числа a2 – a1, a3 – a2, …, a20 – a19. Сумма этих 19 натуральных чисел равна a20 – a1, то есть меньше 70 – 1. Но если предположить, что среди них нет четырёх равных, то там не более трёх единиц, трёх двоек, …, трёх шестерок и еще одно число, не меньшее 7. Сумма таких чисел не меньше, чем 3 • (1 + 2 + 3 + 4 + 5 + 6) + 7 = 70. Получили противоречие, доказывающее, что четыре равных разности найдутся даже среди выписанных 19 разностей соседних чисел.
Задача 13: В последовательности 2, 0, 0, 0, 2, 2, 4,…каждый член, начиная с пятого, равен последней цифре суммы предшествующих четырёх членов. а) Встретятся ли в этой последовательности еще раз подряд 4 цифры 2, 0, 0, 0? б) Встретятся ли в ней четыре подряд цифры 0, 0, 8, 2 ? Решение: а) Да. б) Да. Последовательность рано или поздно зациклится, потому что четверка последовательных цифр однозначно определяет следующую цифру. При этом последовательность обратима с любого места, то есть в ее период входят все цифры, включая самые первые. Цифры 0,0,8,2 встретятся в ней как раз перед вторым появлением четверки 2,0,0,0, потому что если продлить вправо 0,0,8,2, то последовательно получим 0,0 и 0.
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 6 класс >> Принцип Дирихле-2. Сначала сосчитаем | Убрать решения |