 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Геометрические неравенства-1 | Убрать решения |
|
|
| Материалы Кировской ЛМШ, 2000 г, 7 класс. Геометрические неравенства-1 |
|
|

а) против большей стороны лежит больший угол;
б) против большего угла лежит большая сторона.
Задача 3: а) Докажите, что сумма любых двух сторон треугольника больше третьей стороны (неравенство треугольника).б) Докажите, что в треугольнике длина любой стороны больше разности длин двух других сторон.
Задача 4: Докажите, что в выпуклом четырехугольнике сумма диагоналей больше полупериметра. Задача 5: Докажите, что медиана треугольника:а) больше разности полупериметра и стороны, на которую она опущена;
б) меньше полусуммы его сторон, выходящих из той же вершины.
Задача 6: Четыре дома расположены в вершинах выпуклого четырехугольника. Где нужно построить колодец, чтобы сумма расстояний от него до всех домов была наименьшей. (А есть ли такая точка в невыпуклом четырехугольнике?) Задача 7: Докажите, что ломаная длиннее отрезка, соединяющего ее концы. Задача 8: а) Точка B1 лежит на стороне AB треугольника ABC. Докажите, что периметр треугольника AB1C меньше, чем периметр треугольника ABC.б) Точка 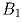 лежит внутри треугольника ABC. Докажите, что периметр
треугольника AB1C меньше, чем периметр треугольника ABC.
лежит внутри треугольника ABC. Докажите, что периметр
треугольника AB1C меньше, чем периметр треугольника ABC.
в) Треугольник A1B1C1 лежит внутри треугольника ABC. Докажите, что периметр треугольника A1B1C1 меньше, чем периметр треугольника ABC. (Как можно обобщить эту задачу?)
Задача 9: В выпуклом четырехугольнике ABCD угол A равен углу B, а угол D больше угла C. Докажите, что BC > AD. Задача 10: Три дома соединены дорожками. Внутри треугольника, образованного дорожками, построена беседка. От беседки к каждому из домов ведет прямая тропинка. Требуется заасфальтировать либо все дорожки, либо все тропинки. Докажите, чтоа) если покрывать тропинки асфальтом в два слоя, то на тропинки уйдет асфальта больше, чем на дорожки;
б) а если их покрывать в один слой, то меньше.
Задача 11: Докажите, что расстояние от любой точки до любой вершины квадрата не больше суммы расстояний от нее до остальных вершин.Задача 12: Дан угол и точка внутри него. Она отражается относительно сторон угла, и получившиеся точки соединяются отрезком. Докажите, что часть этого отрезка, высекаемая углом, составляет меньше половины его длины. Задача 13: Имеются два равнобедренных треугольника с равными боковыми сторонами. Докажите, что основание меньше у того треугольника, у которого меньше противолежащий основанию угол. Задача 14: Построить треугольник наименьшего периметра по данному основанию и опущенной на него высоте. Задача 15: Существует ли выпуклый многоугольник, в котором сумма длин диагоналей равна периметру? Задача 16: В правильный треугольник впишите треугольник наименьшего периметра так, чтобы его вершины попали на разные стороны, а одна – в середину стороны. Задача 17: На биссектрисе угла отмечена точка. Провести через нее отрезок минимальной длины с концами на сторонах угла.
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Геометрические неравенства-1 | Убрать решения |