 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Неравенство треугольника | Убрать решения |
|
|
| Разное. Материалы Кировской ЛМШ, 2001 г, 7 класс. Неравенство треугольника |
|
|
Решение: Ответ: 4.
Задача 2: Докажите, что длина любой стороны треугольника не превосходит его полупериметра.
Решение: Обозначим длины сторон треугольника через a, b, c. Так как b + c > a, то a + b + c > 2a.
Задача 3: Найдите внутри выпуклого четырёхугольника точку, такую, что сумма расстояний от нее до вершин минимальна.
Решение: Так как четырёхугольник выпуклый, то его диагонали пересекаются в точке O. Обозначим вершины четырёхугольника через A, B, C и D (по часовой стрелке). Тогда сумма расстояний от O до вершин равна сумме длин диагоналей AC и BD. Но для любой другой точки P имеем, во-первых, что сумма расстояний от P до вершин не меньше AC + BD, а во-вторых, либо PA + PC > AC, либо PB + PD > BD. Значит эта сумма равна AC + BD только если P совпадает с точкой O. Значит, точка O – искомая. Задача 4: Докажите, что
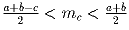 .
.Задача 5: Докажите, что в выпуклом четырёхугольнике сумма длин диагоналей больше его полупериметра и меньше периметра.
Решение: Пусть диагонали пересекаются в точке O. Требуемые неравенства легко выводятся из неравенств треугольника для треугольников OAB, OBC, OCD, ODA и для треугольников ABC, BCD, CDA и DAB.
Задача 6: Докажите, что в выпуклом пятиугольнике сумма длин диагоналей больше периметра и меньше удвоенного периметра. Задача 7: Внутри треугольника взяли две произвольные точки. Докажите, что расстояние между ними не превосходит полупериметра треугольника.
Решение: Продолжите отрезок, соединяющий эти точки, в обе стороны до пересечения с контуром треугольника. Задача 8: На сторонах единичного квадрата отмечены 4 точки, по одной на каждой стороне. Докажите, что периметр образованного ими четырёхугольника больше двух.
Задача 9: В четырёхугольнике ABCD ∠ ADC = 90. Докажите, что 2DB ≤ PABC.
Задача 10: Грибник выходит из леса в заданной точке. Ему надо дойти до шоссе, которое представляет собой прямую линию, и зайти обратно в лес в другой заданной точке. Как ему сделать это, пройдя по самому короткому пути?
Решение: Обозначим точку, в которой грибник выходит из леса, через A, а точку, в которой он должен войти в лес, через B. Отразим точку A симметрично относительно прямой-шоссе и получим точку A′. Тогда из любого пути AKB (K – это точка, в которой грибник выходит на шоссе) можно, отразив симметрично относительно шоссе его участок AK, получить равный ему по длине путь A′KB, длина которого по неравенству треугольника не меньше A′B.
Следовательно, искомая точка K, в которой грибник должен подойти к шоссе – это точка пересечения A′B и шоссе.
Задача 11: Точку M, лежащую внутри угла, отразили симметрично относительно сторон этого угла, в результате чего получились точки M1 и M2. Докажите, что внутри угла содержится не более половины отрезка M1M2.| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Неравенство треугольника | Убрать решения |