 |
 |
|
| Задачная база >> Международные соревнования >> Балканская МО >> 1999 | Показать решения |
|
|
| Международные соревнования. Балканская МО. 1999 |
|
|
Около остроугольного треугольника ABC описана окружность. Точка D – середина дуги BC, не содержащей точки A. Точки E и F симметричны точке D относительно прямой BC и центра описанной окружности O соответственно. Точка K – середина отрезка EA. Докажите, что
a) середины сторон треугольника ABC и точка K лежат на одной окружности
b) Прямая, проходящая через точку K и середину отрезка BC перпендикулярна прямой AF.
Задача 2:
Пусть p – простое число такое, что p – 2 делится на 3. Пусть S – множество чисел, представимых в виде y² – x³ – 1, где x и y – целые числа, 0 ≤ x,y ≤ p – 1. Докажите, что не менее p – 1 элементов множества S делятся на p.
Задача 3:
Пусть ABC – остроугольный треугольник, M, N и P – основания перпендикуляров, опущенных из центра масс G треугольника ABC к сторонам AB, BC и CA соответственно. Докажите, что
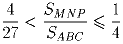
Задача 4:
Пусть x0 = 0 ≤ x1 ≤ x2 ≤ x3 ≤ … ≤ xn ≤ … – неубывающая последовательность неотрицательных целых чисел таких, что для любого целого неотрицательного числа k количество членов не превосходящих k конечно, обозначим это количество через yk. Докажите, что для любых натуральных чисел m и n выполняется неравенство
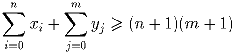
| Задачная база >> Международные соревнования >> Балканская МО >> 1999 | Показать решения |