Задача 1:
[ФРГ] Пусть p
n(k) – число перестановок множества из n
(n ≥ 1) элементов, имеющих ровно k неподвижных точек. Докажите,
что
p
n(1) + 2 • p
n(2) + … + n • p
n(n) = n!
Задача 2:
[СССР] Продолжение биссектрисы AL (L ∈ BC)
остроугольного треугольника ABC пересекает описанную
вокруг него окружность в точке N (N не совпадает с A). Из
точки L на стороны AB и AC опущены перпендикуляры LK и LM.
Докажите, что площади четырехугольника AKNM и треугольника
ABC равны.
Задача 3:
[ФРГ] Пусть x
1,x
2, … ,x
n – действительные числа
и
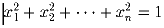
. Докажите, что для любого целого числа
k ≥ 2 существуют целые числа a
1,a
2, … ,a
n, не все равные
нулю, |a
i| ≤ k – 1,i = 1,2, … ,n, и такие, что
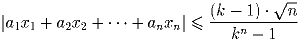
Задача 4:
[Вьетнам] Пусть
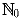
– множество целых неотрицательных
чисел. Докажите, что не существует функции
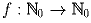
такой, что f(f(n)) = n + 1987 для любого
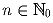
.
Задача 5:
[ГДР] Докажите, что для каждого натурального числа
n, n ≥ 3, можно выбрать на плоскости n точек так, чтобы
выполнялись два условия:
а) расстояние между любыми двумя точками было
иррациональным числом;
б) любые три точки являлись вершинами невырожденного
треугольника, площадь которого выражалась бы рациональным
числом.
Задача 6:
[СССР, В.Ф.Лев] Пусть n ≥ 2 – натуральное число.
Докажите, что если числа k² + k + n – простые для каждого целого
k,
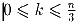
, то числа k² + k + n –
простые для каждого
целого k, 0 ≤ k ≤ n – 2.


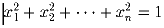 . Докажите, что для любого целого числа
k ≥ 2 существуют целые числа a1,a2, … ,an, не все равные
нулю, |ai| ≤ k – 1,i = 1,2, … ,n, и такие, что
. Докажите, что для любого целого числа
k ≥ 2 существуют целые числа a1,a2, … ,an, не все равные
нулю, |ai| ≤ k – 1,i = 1,2, … ,n, и такие, что 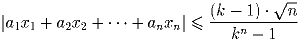
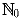 – множество целых неотрицательных
чисел. Докажите, что не существует функции
– множество целых неотрицательных
чисел. Докажите, что не существует функции 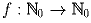 такой, что f(f(n)) = n + 1987 для любого
такой, что f(f(n)) = n + 1987 для любого 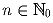 .
Задача 5:
[ГДР] Докажите, что для каждого натурального числа
n, n ≥ 3, можно выбрать на плоскости n точек так, чтобы
выполнялись два условия:
.
Задача 5:
[ГДР] Докажите, что для каждого натурального числа
n, n ≥ 3, можно выбрать на плоскости n точек так, чтобы
выполнялись два условия: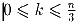 , то числа k² + k + n –
простые для каждого
целого k, 0 ≤ k ≤ n – 2.
, то числа k² + k + n –
простые для каждого
целого k, 0 ≤ k ≤ n – 2.