Задача 1:
(5–7)
Бывают ли натуральные числа, произведение цифр которых
равно 1986,?
Задача 2:
(5–7)
Найти две обыкновенные дроби — одну со знаменателем 8,
другую со знаменателем 13 такие, чтобы они не были равны, но
разность между большей и меньшей из них была как можно меньше.
Задача 3:
(5–7)
За круглым столом сидело а) 15; б) 20 человек. Они хотят
пересесть так, чтобы те, кто раньше сидел рядом, теперь сидели бы
через два человека. Возможно ли это?
Задача 4:
(8–9)
В компании из k человек (k > 3) у каждого появилась
новость, известная ему одному. За один телефонный разговор двое
сообщают друг другу все известные им новости. Докажите, что за
2k – 4 разговора все они могут узнать все новости.
Задача 5:
(8–9)
Через данную точку на плоскости проводятся всевозможные
прямые, пересекающие данную окружность. Найти геометрическое
место середин получившихся хорд.
Задача 6:
(8–9)
Известно, что a + b + c = 5 и ab + bc + ac = 5.
Чему может равняться a² + b² + c²,?
Задача 7:
(8–9)
На плоскости отмечено 5 точек с целыми координатами.
Докажите, что середина по крайней мере одного из соединяющих их
отрезков также имеет целые координаты.
Задача 8:
(5–7)
Вершины выпуклого пятиугольника соединены через
одну. Найдите сумму углов при вершинах получившейся звезды.
Задача 9:
(5–7)
Верно ли, что из любых 10 отрезков найдутся три,
из которых можно составить треугольник?
Задача 10:
(5–7)
Квадратная площадь размером 100,м × 100,м
выложена квадратными плитами 1,м × 1,м четырех цветов:
белого, красного, черного и серого — так, что никакие две плиты
одинакового цвета не соприкасаются друг с другом (то есть не имеют
общей стороны или вершины). Сколько может быть красных плит?
Задача 11:
(5–7)
Отметьте несколько точек и несколько прямых так,
чтобы на каждой прямой лежало ровно три отмеченные точки и через
каждую точку проходило ровно три отмеченные прямые.
Задача 12:
(5–7)
Точку внутри квадрата соединили с вершинами
— получились четыре треугольника, один из которых равнобедренный
с углами при основании (стороне квадрата) 15. Докажите,
что противоположный ему треугольник правильный.
Задача 13:
(5–7)
a
1, a
2, a
3, a
4, a
5, a
6 —
последовательные стороны шестиугольника, все углы которого равны.
Докажите, что a
1 – a
4 = a
3 – a
6 = a
5 – a
2.
Задача 14:
(8–9)
«Крокодилом" называется фигура, ход которой
заключается в прыжке на клетку, в которую можно попасть сдвигом на
одну клетку по вертикали или горизонтали, а затем на
N клеток в перпендикулярном направлении
(при N = 2 «крокодил" — это шахматный конь).
При каких N «крокодил" может пройти с любой клетки
бесконечной шахматной доски на любую другую?
Задача 15:
(8–9)
Фабрика окрашивает кубики в 6 цветов (каждую
грань в свой цвет, набор цветов фиксирован). Сколько
разновидностей кубиков можно изготовить?
Задача 16:
(8–9)
Докажите, что произведение ста последовательных
натуральных чисел не может быть сотой степенью натурального числа.
Задача 17:
(8–9)
Из шахматной доски вырезали одну угловую клетку.
На какое наименьшее число равновеликих треугольников можно
разрезать эту фигуру?
Задача 18:
(8–9)
a, b, c, d — стороны четырехугольника
(в любом порядке), S — его площадь. Докажите, что
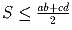
.


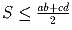 .
.