 |
 |
|
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1986 | Убрать решения |
|
|
| Турнир имени Ломоносова. Конкурс по математике. 1986 |
|
|
Задача 2: (5–7) Найти две обыкновенные дроби — одну со знаменателем 8, другую со знаменателем 13 такие, чтобы они не были равны, но разность между большей и меньшей из них была как можно меньше. Решение: Пусть первая дробь равна
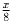 ,, а
вторая —
,, а
вторая — 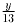 ,. Тогда разность между
большей и меньшей из них равна
,. Тогда разность между
большей и меньшей из них равна
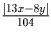 ,. В числителе полученной дроби
стоит целое положительное число. Поэтому она не может быть меньше
,. В числителе полученной дроби
стоит целое положительное число. Поэтому она не может быть меньше
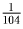 ,. А быть равной
,. А быть равной
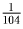 — может. Для этого нужно, чтобы
числитель был равен единице. Это выполняется, если, например,
x = 3, y = 5 (или x = 5, y = 8).
— может. Для этого нужно, чтобы
числитель был равен единице. Это выполняется, если, например,
x = 3, y = 5 (или x = 5, y = 8).Задача 3: (5–7) За круглым столом сидело а) 15; б) 20 человек. Они хотят пересесть так, чтобы те, кто раньше сидел рядом, теперь сидели бы через два человека. Возможно ли это? Решение: а) Пронумеруем все места за столом по кругу и всех сидящих соответственно занимаемым местам. Будем считать, что нам удалось всех пересадить требуемым образом. Без ограничения общности можно считать, что человек 1 остался сидеть на своем месте. Если это не так, то этого можно добиться поворотом стола; при этом условие задачи нарушиться, очевидно, не может. Человек 2 может сидеть либо на месте 4, либо на месте 13. Разберем первый из этих случаев (рис. 15 a). В этом случае для третьего есть единственное место, удовлетворяющее условию — 7. Далее, 4-й может сидеть только на месте 10, 5-й — на месте 13. При этом для 6-го единственное возможное место — 1. Но оно уже занято первым. Значит, рассадить людей требуемым образом не удастся. Второй случай разбирается аналогично.
б) Опять пронумеруем места подряд вокруг стола и людей соответственно занимаемым местам. На рис. 15 б) показан способ пересадить людей, удовлетворяющий условиям задачи.
Задача 4: (8–9) В компании из k человек (k > 3) у каждого появилась новость, известная ему одному. За один телефонный разговор двое сообщают друг другу все известные им новости. Докажите, что за 2k – 4 разговора все они могут узнать все новости. Решение: Передача информации может быть осуществлена следующим образом. Рассмотрим некоторых четверых людей в компании — назовем их A, B, C, D. Пусть сначала все члены компании, кроме B, C и D звонят A и сообщают ему свои новости. Это потребует k – 4 звонка. Затем между собой говорят A и B, а также C и D. После этого A говорит с C, а B с D, в результате чего все четверо будут знать все новости. За оставшиеся 2n – 4 звонка A сообщает их всем остальным.
Задача 5: (8–9) Через данную точку на плоскости проводятся всевозможные прямые, пересекающие данную окружность. Найти геометрическое место середин получившихся хорд. Решение: Искомое геометрическое место середин хорд — это дуга окружности, построенной на отрезке, соединяющем данную точку и центр данной окружности, как на диаметре, лежащая внутри данной окружности (в частности, если точка лежит внутри окружности, то получается вся окружность).
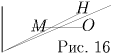
Пусть O — центр данной окружности, M — данная точка, l — произвольная прямая, пересекающая окружность и проходящая через точку M, H — середина хорды, получающейся при пересечении прямой окружности (рис. 16). Воспользуемся известной теоремой: радиус перпендикулярен хорде тогда и только тогда, когда он делит ее пополам. Из этой теоремы следует, что угол MHO — прямой. Из обратной теоремы о величине угла, опирающегося на диаметр, следует, что точка H лежит на окружности с диаметром OM. Обратно, пусть H — точка, лежащая на окружности с диаметром OM и внутри данной окружности. По прямой теореме о величине угла, опирающегося на диаметр, получаем, что прямые MH и HO перпендикулярны. Применив теорему о радиусе, перпендикулярном хорде, еще раз, получим, что k — середина хорды, образованной прямой, проходящей через точку M.
Задача 6: (8–9) Известно, что a + b + c = 5 и ab + bc + ac = 5. Чему может равняться a² + b² + c²,? Решение: Воспользуемся формулой (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac. Имеем a² + b² + c² = (a + b + c)² – 2(ab + bc + ac) = 5² – 2 • 5 = 15.
Задача 7: (8–9) На плоскости отмечено 5 точек с целыми координатами. Докажите, что середина по крайней мере одного из соединяющих их отрезков также имеет целые координаты. Решение: Воспользуемся тем, что координаты середины отрезка с концами (x1,y1) и (x2,y2) равны
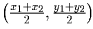 (докажите это). Среди пяти точек с целыми координатами найдутся
три, абсциссы которых имеют одинаковую четность (то есть либо все
четны, либо все нечетны). Действительно, если бы точек с четными
абсциссами было не больше двух и с нечетными абсциссами не больше
двух, то всего точек было бы не больше четырех. Аналогично, среди
этих трех точек найдутся две с ординатами одной четности. Пусть
это точки (x1,y1) и (x2,y2). Поскольку x1 и x2 либо
оба четны, либо оба нечетны, то x1 + x2 — четное, и
(докажите это). Среди пяти точек с целыми координатами найдутся
три, абсциссы которых имеют одинаковую четность (то есть либо все
четны, либо все нечетны). Действительно, если бы точек с четными
абсциссами было не больше двух и с нечетными абсциссами не больше
двух, то всего точек было бы не больше четырех. Аналогично, среди
этих трех точек найдутся две с ординатами одной четности. Пусть
это точки (x1,y1) и (x2,y2). Поскольку x1 и x2 либо
оба четны, либо оба нечетны, то x1 + x2 — четное, и
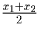 — целое. Аналогично,
— целое. Аналогично,
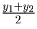 — целое. Утверждение
доказано.
— целое. Утверждение
доказано.Задача 8: (5–7) Вершины выпуклого пятиугольника соединены через одну. Найдите сумму углов при вершинах получившейся звезды. Решение:
Пусть ABCDE исходный пятиугольник, а A′B′C′D′E′ — пятиугольник, образованный при пересечении его диагоналей (рис. 17). Рассмотрим сумму углов пяти треугольников ACB′, BDC′, CED′, DAE′ и EBA′. В эту сумму входят по два раза углы звезды ACEBD и по разу углы пятиугольника A′B′C′D′E′. Поскольку сумма углов любого треугольника равна 180, а пятиугольника — 540. Отсюда выводим, что искомая сумма углов равна 180.
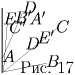
Задача 9: (5–7) Верно ли, что из любых 10 отрезков найдутся три, из которых можно составить треугольник? Решение:
Рассмотрим 10 отрезков с длинами 1, 2, 4, …, 512 (каждый следующий вдвое длиннее предыдущего). Тогда пусть a, b и c — длины любых трех из данных отрезков, причем a < b < c. Тогда можно утверждать, что b ≤ ½c,, a < ½c,. Сложив последние два неравенства, получаем b + a < c. Согласно неравенству треугольника (см. Т17), из отрезков с длинами a, b и c нельзя составить треугольник.
Задача 10: (5–7) Квадратная площадь размером 100,м × 100,м выложена квадратными плитами 1,м × 1,м четырех цветов: белого, красного, черного и серого — так, что никакие две плиты одинакового цвета не соприкасаются друг с другом (то есть не имеют общей стороны или вершины). Сколько может быть красных плит? Решение:
Разобьем каждую сторону квадрата, ограничивающего данную площадь на 50 равных частей и соединим соответствующие точки деления на противоположных сторонах. В результате вся площадь разобьется на 2500 квадратиков 2,м × 2,м, каждый из которых состоит из четырех плиток с общей вершиной. Значит, каждый из этих квадратиков может содержать не более одной красной плитки, и, тем самым, количество красных плиток не может превышать 2500. С другой стороны, мы покажем, что ровно 2500 красных плиток быть может. Для этого нужно собрать блок 2 × 2 из четырех плит разного цвета, и замостить 2500 такими блоками всю площадь, следя за тем, чтобы все блоки были ориентированы одинаково.
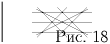
Задача 11: (5–7) Отметьте несколько точек и несколько прямых так, чтобы на каждой прямой лежало ровно три отмеченные точки и через каждую точку проходило ровно три отмеченные прямые. Решение:
См. рис. 18.
Задача 12: (5–7) Точку внутри квадрата соединили с вершинами — получились четыре треугольника, один из которых равнобедренный с углами при основании (стороне квадрата) 15. Докажите, что противоположный ему треугольник правильный. Решение:
Обозначим наш квадрат ABCD, а данную внутри него точку M. Пусть ∠ MDC = ∠ MCD = 15. Решим обратную задачу. Построим на стороне AB квадрата равносторонний треугольник ABN так, чтобы вершина N лежала внутри квадрата (рис. 19). Тогда треугольник CNB равнобедренный с вершиной B. Его угол при вершине равен 30, следовательно, угол при основании равен (180 – 30)/2 = 75. Отсюда находим ∠ DCN = 90 – 75 = 15. Аналогично получаем ∠ CDN = 15. По условию ∠ DCM = ∠ CDM = 15. Значит, точка N лежит на луче CM и на луче DM, тем самым, совпадает с M.
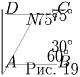
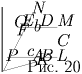
Задача 13: (5–7) a1, a2, a3, a4, a5, a6 — последовательные стороны шестиугольника, все углы которого равны. Докажите, что a1 – a4 = a3 – a6 = a5 – a2.
Решение:
Продолжим стороны данного шестиугольника ABCDEF до пересечения друг с другом. Шестиугольник оказался представленным в виде пересечения двух равносторонних треугольников KMO и LNP (рис. 20) со сторонами b и c соответственно. Объединение этих треугольников представляет собой шестиконечную звезду, лу-чи которой ABK, BCL, CDM, DEN, EFO и FAP являются равносторонними треугольниками. Можем записать
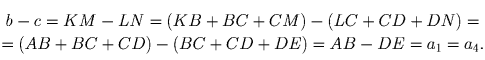
Аналогично получаем, b – c = a3 – a6 и b – c = a5 – a2, откуда следует требуемое равенство.
Задача 14: (8–9) «Крокодилом" называется фигура, ход которой заключается в прыжке на клетку, в которую можно попасть сдвигом на одну клетку по вертикали или горизонтали, а затем на N клеток в перпендикулярном направлении (при N = 2 «крокодил" — это шахматный конь). При каких N «крокодил" может пройти с любой клетки бесконечной шахматной доски на любую другую?
Решение:
Будем считать, что рассматриваемая бесконечная шахматная доска, как и обычная, раскрашена в белый и черный цвета в шахматном порядке. Тогда при нечетном N «крокодил" будет ходить только по клеткам одного цвета, и, тем самым не может пройти на любую клетку.
Докажем теперь, что при четном N «крокодил" может пройти с любой клетки на любую. Очевидно, для этого достаточно доказать, что он может пройти с любой клетки на соседнюю (смежную по стороне). Покажем, как пройти из клетки в соседнюю с ней сверху. Первым ходом ходим на одну клетку вправо и N клеток вверх, а вторым — на одну вправо и N вниз. Так мы окажемся на две клетки правее исходной. Повторим эту пару ходов N/2 раз (тогда мы окажемся на N клеток правее исходной), после чего пойдем на одну клетку вверх и N влево. Мы оказались в клетке, соседней с исходной.
Задача 15: (8–9) Фабрика окрашивает кубики в 6 цветов (каждую грань в свой цвет, набор цветов фиксирован). Сколько разновидностей кубиков можно изготовить? Решение:
Предположим, что процедура раскраски кубика происходит следующим образом: непокрашенный кубик устанавливается в станок в некоторое фиксированное положение, а затем последовательно красятся его грани в определенном порядке: нижняя, верхняя, правая, левая, передняя, задняя. Посчитаем сначала, сколькими способами можно осуществить такую раскраску. Нижнюю грань мы можем покрасить любой из шести красок. После этого для верхней грани останется лишь пять возможностей, поскольку одна краска уже использована. Затем правую грань мы сможем покрасить четырьмя способами, левую — тремя, переднюю двумя, а выбора для цвета задней грани нет — ее мы вынуждены покрасить в оставшийся неиспользованным цвет. Поэтому всего способов раскраски 6 • 5 • 4 • 3 • 2 = 720. Однако же, получающихся разновидностей кубиков гораздо меньше, поскольку установить кубик в фиксированное положение можно различными способами. Сколькими? Кубик можно установить на любую из шести граней и затем повернуть одним из четырех способов — получаем всего 6 • 4 = 24 способа. Поэтому разновидностей кубиков в 24 раза меньше, чем способов раскраски, их всего 30.
Задача 16: (8–9) Докажите, что произведение ста последовательных натуральных чисел не может быть сотой степенью натурального числа. Решение:
Предположим, что для некоторых натуральных n и k
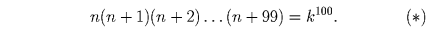
Задача 17: (8–9) Из шахматной доски вырезали одну угловую клетку. На какое наименьшее число равновеликих треугольников можно разрезать эту фигуру? Решение:
На рис. 21 показано, как разрезать данную фигуру на 18
равновеликих треугольников. Докажем, что это число — максимально
возможное. Примем за единицу площадь одной клетки. Данная фигура
представляет собой невыпуклый шестиугольник ABCDEF площади 63 с
углом 270 в вершине D (рис. 22). Если мы имеем разбиение
фигуры на треугольники, то, очевидно, что точка D должна
принадлежать по крайней мере двум треугольникам, причем у одного
из них сторона лежит на прямой DE, а у другого — на DC.
Более того, по крайней мере для одного из них она лежит на
соответствующем отрезке. Для определенности предположим, что это
треугольник DKL, причем K ∈ [DC]. Тогда основание DK этого
треугольника не больше DC = 1, а высота — не больше BC = 7.
Поэтому площадь треугольника DKL не больше 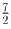 .
По условию, мы имеем разбиение данной фигуры на равновеликие
треугольники. Поскольку площадь одного треугольника не больше
.
По условию, мы имеем разбиение данной фигуры на равновеликие
треугольники. Поскольку площадь одного треугольника не больше
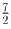 , то всего треугольников не меньше
, то всего треугольников не меньше
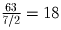 .
.
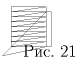
Задача 18: (8–9) a, b, c, d — стороны четырехугольника (в любом порядке), S — его площадь. Докажите, что
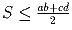 .
.Решение:
Прежде всего заметим, что достаточно ограничиться рассмотрением случая выпуклого четырехугольника. Действительно, для любого невыпуклого четырехугольника мы можем построить выпуклый с теми же длинами сторон, но большей площади, отразив две его стороны относительно диагонали, лежащей снаружи (рис. 23,а).
Предположим сначала, что стороны четырехугольника идут в указанном
порядке. Разобьем четырехугольник диагональю на два треугольника
со сторонами a, b, l и c, d, l и площадями S1 и
S2 соответственно (рис. 23,б). Площадь треугольника не меньше
половины произведения двух его сторон. Это следует из того, что
сторона треугольника не меньше высоты, опущенной на другую
сторону. Сложив неравенства 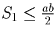 и
и 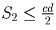 , получим требуемое неравенство.
, получим требуемое неравенство.
Пусть теперь стороны a и b четырехугольника несмежны. Разобьем снова данный четырехугольник на два треугольника диагональю. Теперь треугольник, имеющий стороны a и d оставим на месте, а имеющий стороны b и c отразим относительно серединного перпендикуляра к проведенной диагонали (рис. 23,в). Получим четырехугольник той же площади, с теми же сторонами, но идущими в другом порядке (стороны a и b, а также c и d в нем смежны). Для такого четырехугольника неравенство нами уже доказано. А из этого и следует неравенство для рассматриваемого исходного четырехугольника.
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1986 | Убрать решения |