 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Ирландия >> 2001 | Показать решения |
|
|
| Ирландская математическая олимпиада.. 2001 |
|
|
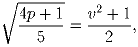
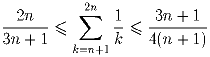
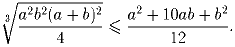
Докажите также, что при всех вещественных a и b
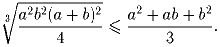
Задача 6: Найдите наименьшее натуральное число a такое, что 55n + a • 32n делится на 2001 при некотором нечётном n.
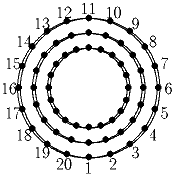
Задача 7: Три замкнутых в кольца нити расположены концентрично, как показано на рисунке. На каждой нити надеты 20 бусины, из которых 10 чёрных и 10 белых. На каждом нити позиции бусин помечены числами от 1 до 20, начиная с низу против часовой стрелки.
Будем говорить, что на позиции i есть совпадение, если все три бусины на позиции i одного цвета. Разрешается перемещать бусины вдоль нитей. Докажите, что можно добиться конфигурации, при которой будет не менее 5 совпадений.
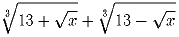
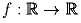 , что
f(x + f(y)) = f(x) + y
при всех натуральных x и y.
, что
f(x + f(y)) = f(x) + y
при всех натуральных x и y.
| Задачная база >> Национальные зарубежные олимпиады >> Ирландия >> 2001 | Показать решения |