 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1996 >> 1 тур | Убрать решения |
|
|
| Польская математическая олимпиада.. 1996. 1 тур |
|
|
Найдите все натуральные n, такие, что уравнение 2 sin nx = tg x + ctg x имеет вещественный корень.
Задача 2:Число называется палиндромом если его десятичная запись одинаково читается как слева направо, так и справа налево. Пусть xn – последовательность всех палиндромов в порядке возрастания. Найдите все простые числа, которые делят по крайней мере одну разность xk + 1 – xk.
Решение:
Для не делящегося на 10 числа A через A′ обозначим
число, получающееся «переворачиванием» A (таким образом A –
палиндром, если A = A′). Тогда любой палиндром имеет вид
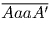 , либо
, либо 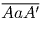 (a – цифра).
Если a ≠ 9, то следующий палиндром имеет вид
(a – цифра).
Если a ≠ 9, то следующий палиндром имеет вид 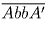 ,
либо
,
либо 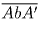 , где b = a + 1. В таком случае разность
соседних палиндромов имеет вид 110 … 0, либо 100 … 0 соответственно.
Если a = 9, то следующий палиндром имеет вид
, где b = a + 1. В таком случае разность
соседних палиндромов имеет вид 110 … 0, либо 100 … 0 соответственно.
Если a = 9, то следующий палиндром имеет вид
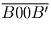 (
(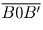 ), где B = A + 1. Опять же
разность равна 110 … 0, следовательно, простые числа делящие
разность соседних палиндромов – 2, 5 или 11.
), где B = A + 1. Опять же
разность равна 110 … 0, следовательно, простые числа делящие
разность соседних палиндромов – 2, 5 или 11.
Задача 3:
В группе из kn человек у каждого не менее (k – 1)n знакомых. Докажите, что можно выбрать k + 1 человека так, что все они будут попарно между собой знакомы.
Задача 4:Касательная к окружности, вписанной в равносторонний треугольник ABC, пересекает стороны AB и AC в точках D и E соответственно. Докажите, что AD/DB + AE/EC = 1.
Задача 5:В треугольнике ABC угол A – тупой. PQ – отрезок, серединой
которого является точка A. Докажите, что
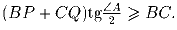
Даны две последовательности натуральных чисел: геометрическая прогрессия со знаменателем q > 1 и арифметическая прогрессия с разностью r > 0, где q и r взаимно простые целые числа. Докажите, что если хотя бы одно число принадлежит обеим прогрессиям, то таких чисел бесконечно много.
Задача 7:Неотрицательные числа a, b, c, p, q, r удовлетворяют следующим
условиям: 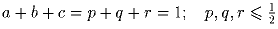 . Докажите, что
8abc ≤ pa + qb + rc и определите когда достигается равенство.
. Докажите, что
8abc ≤ pa + qb + rc и определите когда достигается равенство.
Луч света выходит из центра квадрата и отражается от его сторон в соответствии с законом угол падения луча равен углу отражения. Через некоторое время луч вернулся в центр квадрата, при этом он ни разу не побывал ни в вершинах ни в его центре. Докажите, что количество отражений луча от стенок нечетно.
Остаток от деления многочлена f с целыми коэффициентами на квадратный трехчлен x² – 12x + 11 равен 990x – 889. Докажите, что у f нет целых корней.
Задача 10:Докажите, что уравнение xx = y³ + z³ имеет бесконечно много решений в натуральных числах.
Задача 11:В соревнованиях по прыжкам с трамплина участвовало 65 человек. Каждый спортсмен прыгает только один раз. Допустим, что все результаты прыжков различны. В каждый момент соревнования лидером назовем человека, чей результат наиболее высокий на данный момент. Через p обозначим вероятность того, что за все соревнование лидер сменится всего один раз. Докажите, что если порядок прыжков определен случайным образом, то p > 1/16.
Задача 12:Существуют ли два таких равных куба, центры которых совпадают и каждая сторона одного куба имеет общую точку с каждой стороной второго?
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1996 >> 1 тур | Убрать решения |