 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1996 >> 2 тур | Показать решения |
|
|
| Польская математическая олимпиада.. 1996. 2 тур |
|
|
Верно ли, что каждый многочлен с целыми коэффициентами можно представить в виде суммы кубов многочленов с целыми коэффициентами?
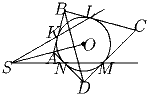
Задача 2:Окружность с центром в точке O, вписанная в выпуклый четырехугольник ABCD, касается его сторон AB, BC, CD и DA в точках K, L, M и N соответственно. Прямые KL и MN не параллельны и пересекаются в точке S. Докажите, что BD ⊥ OS.
Докажите, что если a,b,c ≥ 3/4 и a + b + c = 1, то
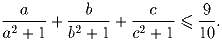
a1,a2, … ,a99 – последовательность цифр. Притом, если an = 1, то an + 1 ≠ 2, а если an = 3, то an + 1 ≠ 4. Докажите, что существуют такие два различных натуральных числа k и l не превосходящие 98, что ak = al и ak + 1 = al + 1.
Задача 5:Найдите все целочисленные решения уравнени x²(y – 1) + y²(x – 1) = 1.
Задача 6:Докажите, что расстояние от произвольной точки внутри
параллелепипеда со сторонами a, b, c до какой-то из его вершин не
превосходит
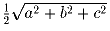
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1996 >> 2 тур | Показать решения |