 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Турецкие олимпиады >> 1996 | Показать решения |
|
|
| Национальные зарубежные олимпиады. Турецкие олимпиады. 1996 |
|
|
An и α n – последовательности натуральных чисел,
притом, любое натуральное x
можно единственным образом представить в виде
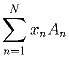 , где все числа xn – целые,
0 ≤ xn ≤ α n и xN ≠ 0.
, где все числа xn – целые,
0 ≤ xn ≤ α n и xN ≠ 0.
Докажите, что 1) существует такое n0, что 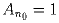 ;
2) Ak ≠ Aj при k ≠ j;
3) если Ak ≤ Aj, то Ak делится на Aj.
;
2) Ak ≠ Aj при k ≠ j;
3) если Ak ≤ Aj, то Ak делится на Aj.
На сторонах AB и CD квадрата ABCD отмечены точки M и N соответственно. Прямые CM и BN пересекаются в точке P, а AN и MD – в точке Q. Докажите, что |PQ| ≥ ½|AB|.
Задача 3:
На прямой покрасили n целочисленных точек. Определите все возможные k такие, что найдется семейство замкнутых попарно непересекающихся отрезков, содержащих все покрашенные точки, притом для каждого отрезка I отношение числа покрашенных точек из I к числу всех целых точек в I равно 1/k.
Задача 4: Дан четырехугольник ABCD и окружность, касающаяся сторон AD, DC и CB в точках K, L и M соответственно. Прямая, проходящая через L параллельно AD пересекает отрезок KM в точке N. P – точка пересечения LN и KC. Докажите, что |PL| = |PN|. Задача 5:
Докажите, что 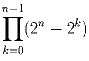 делится на n!.
делится на n!.
Докажите, что не существует такой функции f заданной на множестве вещественных чисел, что f(x + y) > f(x)(1 + yf(x)) для всех x,y.
| Задачная база >> Национальные зарубежные олимпиады >> Турецкие олимпиады >> 1996 | Показать решения |