Задача 1: На острове Невезения, где живут только рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут, существуют три политических партии, причем каждый житель состоит ровно в одной из них. Каждому жителю задали три вопроса: состоите ли вы в первой, состоите ли во второй, состоите ли в третьей партии. На эти вопросы было получено 60%, 50%, 40% [60%, 40%, 30%] утвердительных ответов соответственно. Кого во второй [третьей] партии больше: рыцарей или лжецов?

(Ф.~Назаров)

Задача 2: Можно ли в таблице 3 × 3 расставить числа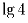 , , 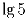…, 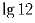[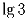, , 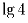…, 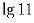] так, чтобы множество сумм чисел этой таблицы по строкам совпадало со множеством сумм чисел по столбцам?

(А.~Храбров)

Задача 3: В ромбе ABCD на отрезке BC нашлась точка E, такая, что AE = CD. Отрезок ED пересекается с описанной окружностью треугольника AEB в точке F. Докажите, что точки A, F и C лежат на одной прямой.

[В ромбе ABCD описанная окружность треугольника BCD пересекает сторону AB в точке E, описанная окружность треугольника AED пересекает отрезок BD в точке F. Докажите, что точки E, F и C лежат на одной прямой.]

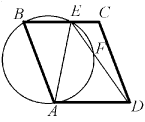
(С.~Берлов)

Задача 4: x и y – вещественные числа из отрезка [0,1/2]. Докажите неравенство: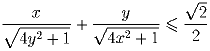

[ x и y – вещественные числа из отрезка [0,2]. Докажите неравенство:

]

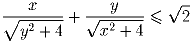
(А.~Голованов)

Задача 5: Дан тетраэдр ABCD. Плоскость  γ  делит пополам двугранный угол при ребре AB и пересекает ребро CD в точке M. При этом оказалось, что отрезок BM – биссектриса угла B треугольника BCD. На ребрах BC и BD выбраны точки K и L, такие, что отрезки AK и AL – высоты треугольников ABC и ABD соответственно. Докажите, что прямая KL перпендикулярна плоскости  γ .

(М.~Пратусевич, К.~Кохась)