 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Олимпиада ЮМШ >> 1999 год >> Городской тур >> Победители олиимпиад | Показать решения |
|
|
| Олимпиада победителей олимпиад |
|
|
Имеется возрастающая последовательность натуральных чисел. Любое натуральное число, которого нет в этой последовательности, является суммой каких-то двух членов этой последовательности. Докажите, что на n-ом месте в последовательности стоит число, не большее .
Задача 2:
Докажите, что всевозможных n-мино (фигурок из n клеточек)
существует не более 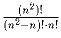 штук.
штук.
Задача 3:
В шахматном королевстве балетмейстер придумал «танец коней». Танцующие кони делают два «правых» шага, а потом один «левый» (шаг заключается в том, что конь скачет на 2 клетки вперед, а потом поворачивает и скачет на 1 клетку вправо, если ход «правый», или на одну клетку влево, если ход «левый»). Может ли конь, танцуя в Большом клетчатом зале, побывать в двух клетках имеющих либо общую сторону, либо общий угол?
Задача 4:
Докажите, что НОД чисел вида p4 – 1, где p – простое число большее 5, равен 240.
Задача 5:
Паша играл в тетрис (в стакан шириной 10 клеток падают фигурки из 4 клеток, если клетки фигурок полностью заполняют какую-либо линию, она исчезает, а верхние клетки съезжают вниз). Перед выходом в школу старший брат посмотрел на экран и запомнил картинку. Придя из школы, он первым делом поинтересовался у брата: «Как игра?», на что услышал – «1999 линеек за это время уничтожил». Брат посмотрел на экран и воскликнул: «Да ведь эта та же картинка, что была перед моим уходом, только вверх ногами!». Докажите, что кто-то из них ошибся.
Задача 6:
Есть три различных натуральных числа, сумма которых равна 45. Всегда ли числа 1,2,3,…,9 можно распределить по 3 группам так, чтобы сумма чисел в первой группе равнялась бы первому числу, во второй – второму, и в третьей – третьему?
Задача 7:
На столе лежит 1999 спичек. За ход первый игрок может взять либо 5, либо 8 спичек; второй – либо 4, либо 6 спичек. Проигрывает тот, кто не может сделать ход. Кто из игроков может обеспечить себе выигрыш, и как он должен для этого играть?
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Олимпиада ЮМШ >> 1999 год >> Городской тур >> Победители олиимпиад | Показать решения |