 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> X, 1995 >> Первый тур | Убрать решения |
|
|
| Десятый Российский Фестиваль Юных Математиков. Адлер-99. Первый тур |
|
|
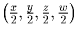 –
решение с меньшей суммой модулей. Получили противоречие.
Задача 2: В треугольнике ABC проведены медианы BD, AK и CE,
которые пересекаются в точке M.
Известно, что
–
решение с меньшей суммой модулей. Получили противоречие.
Задача 2: В треугольнике ABC проведены медианы BD, AK и CE,
которые пересекаются в точке M.
Известно, что 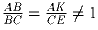 .
Докажите, что окружности, описанные около треугольников ABM
и CBM, касаются прямой AC.
Решение:
Рассмотрим треугольники AEC и AKC. Так как площади их равны, то
EA • EC • sin ( ∠ AEC) = KA • KC sin ( ∠ AKC).
Из условия задачи следует, что EA • EC = KA • KC.
Поэтому sin ( ∠ AEC) = sin ( ∠ AKC).
Так как AB ≠ BC, то AEC ≠ AKC и поэтому
∠ AEC + ∠ AKC = 180.
Но тогда четырехугольник EBKM вписанный, ∠ ABM = ∠ EKM = ∠ MAD,
треугольник ABD подобен треугольнику MAD. Тогда AD/BD = MD/AD, AD² = DM • DB.
Из этого равенства следует, что окружность, описанная около треугольника ABM,
касается прямой AC. Из равенства DC² = DM • DB следует, что окружность,
описанная около треугольника MBC, касается тоже прямой AC.
Задача 3: Можно ли прямоугольник 4 × 1,5 разрезать на 2 части,
которыми оборачивается единичный куб?
Решение:
Можно: разрежем прямоугольник 4 × 1,5 указанным образом.
Тогда легко свернуть каждую часть по пунктирным линиям так, что можно
обернуть «половинку» куба (через центр куба проводится плоскость
параллельная одному из оснований).
.
Докажите, что окружности, описанные около треугольников ABM
и CBM, касаются прямой AC.
Решение:
Рассмотрим треугольники AEC и AKC. Так как площади их равны, то
EA • EC • sin ( ∠ AEC) = KA • KC sin ( ∠ AKC).
Из условия задачи следует, что EA • EC = KA • KC.
Поэтому sin ( ∠ AEC) = sin ( ∠ AKC).
Так как AB ≠ BC, то AEC ≠ AKC и поэтому
∠ AEC + ∠ AKC = 180.
Но тогда четырехугольник EBKM вписанный, ∠ ABM = ∠ EKM = ∠ MAD,
треугольник ABD подобен треугольнику MAD. Тогда AD/BD = MD/AD, AD² = DM • DB.
Из этого равенства следует, что окружность, описанная около треугольника ABM,
касается прямой AC. Из равенства DC² = DM • DB следует, что окружность,
описанная около треугольника MBC, касается тоже прямой AC.
Задача 3: Можно ли прямоугольник 4 × 1,5 разрезать на 2 части,
которыми оборачивается единичный куб?
Решение:
Можно: разрежем прямоугольник 4 × 1,5 указанным образом.
Тогда легко свернуть каждую часть по пунктирным линиям так, что можно
обернуть «половинку» куба (через центр куба проводится плоскость
параллельная одному из оснований). 
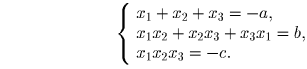
Первый случай: |a| = |b| = |c| ≠ 0, тогда
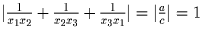 ,
,
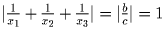 .
Тогда
.
Тогда
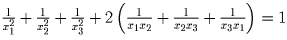 .
Тогда
.
Тогда 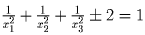 .
Тогда
.
Тогда 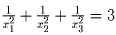 и |x1| = |x2| = |x3| = 1 – противоречие.
и |x1| = |x2| = |x3| = 1 – противоречие.
Второй случай: |a| = |b| = 1. Тогда
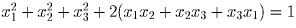 ,
тогда
,
тогда 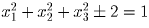 , тогда
, тогда
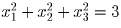 , тогда |x1| = |x2| = |x3| = 1 –
противоречие. Но тогда коэффициентов, равных по модулю не более двух и
уравнение x³ – x = 0 подходит.
, тогда |x1| = |x2| = |x3| = 1 –
противоречие. Но тогда коэффициентов, равных по модулю не более двух и
уравнение x³ – x = 0 подходит.
Задача 5: Имеется три внешне одинаково выглядящие монеты, одна из которых фальшивая, причем неизвестно, легче она или тяжелее настоящей. Можно ли за три взвешивания на чашечных весах без гирь узнать, отрегулированы весы или нет? (У неотрегулированных весов при взвешивании одна из чашек всегда «завышает» вес.) Решение: Ответ: да. Обозначим монеты A, B, C. Под взвешиванием (A,B) подразумеваем, что монета A лежит на левой чашке весов, а монета B – на правой. A > B означает, что левая чашка перевешивает. Вес монеты A будем обозначать m(A).
Если во время первого или второго взвешивания будет равенство, например, A = B, то следующим взвешиванием (B,A) мы, очевидно, выясняем, отрегулированы весы или нет.
Пусть во время первого взвешивания A > B. Вторым взвешиванием делаем (C,A). Если C > A, то весы не отрегулированы. Действительно, если бы весы были отрегулированы, то отсюда следовало бы, что m(C) > m(A) > m(B) – противоречие. Если же C < A, то третьим взвешиванием проводим (B,C). Если B > C или B < C, то весы не отрегулированы (аналогично предыдущему, так как в противном случае мы бы получали m(A) > m(B) > m(C) или m(B) < m(C) < m(A) соответственно. Если же B = C, то весы отрегулированы. Докажем это. Предположим, что весы не отрегулированы. Тогда одна из монет B и C – фальшивая. Без ограничения общности можно считать, что B – фальшивая. Тогда монеты C и A – настоящие. Так как C < A, правая чашка завышает вес. Так как B = C, m(B) > m(C). Посмотрим на A > B. Отсюда m(A) > m(B), то есть настоящая весит больше, чем фальшивая – противоречие. Таким образом, мы разобрали все случаи.
Задача 6: Площадь треугольника с вершинами в узлах целочисленной решетки равна ½. Может ли наименьшая из его сторон быть больше 2000? Решение: Ответ: может. Построим параллелограм ABCD, A(0,0), B( – 10000,1), C(1,0), D(10000, – 1). Одним из искомых треугольников является треугольник ABD (его площадь равна ½, т.к. площадь параллелограмма ABCD равна 1). Задача 7: Шахматная доска 8 × 8 клеток разбита на 32 прямоугольника размера 2 × 1 каждый. Два прямоугольника назовем «соседними», если они имеют более чем одну общую точку. Двое играют на этой доске в следующую игру. В левом нижнем углу стоит фишка первого игрока, в левом верхнем – второго. Игроки ходят по очереди. Начинает первый. Ход заключается в переставлении своей фишки на соседний прямоугольник. Выигрывает тот игрок, который первым доберется до противоположного угла доски. Существует ли такое разбиение доски, при котором при правильной игре обоих игроков выигрывает второй? (Во время игры обе фишки могут оказаться в одном прямоугольнике) . Решение: Да (см.рисунок). При таком разбиении второй игрок доберётся за семь ходов, а первый – не менее, чем за девять.

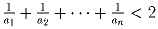 .
Решение: Пусть в условии задачи даны числа даны числа
a1 < a2 < … < an. Докажем индукцией по n более сильный факт:
.
Решение: Пусть в условии задачи даны числа даны числа
a1 < a2 < … < an. Докажем индукцией по n более сильный факт:
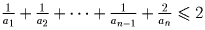 .
База очевидна. Считаем, что для всех
натуральных k < n предположение индукции верно. Переход: если an > 2an – 1, то просто выкинем из набора an. При этом правая часть не
изменится, а левая увеличится на
.
База очевидна. Считаем, что для всех
натуральных k < n предположение индукции верно. Переход: если an > 2an – 1, то просто выкинем из набора an. При этом правая часть не
изменится, а левая увеличится на 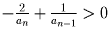 .
Если же an ≤ 2an – 1, то выкинем
an и an – 1, а добавим an – an – 1
(ясно, что если все
суммы были попарно различны, то и новые суммы будут попарно различны). При
этом левая часть увеличится либо на
.
Если же an ≤ 2an – 1, то выкинем
an и an – 1, а добавим an – an – 1
(ясно, что если все
суммы были попарно различны, то и новые суммы будут попарно различны). При
этом левая часть увеличится либо на 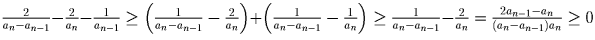 ,
либо на
,
либо на 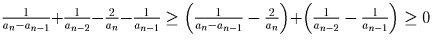 . Переход сделан.
Задача 9: В классе, в котором учатся 20 человек, каждые два либо
дружат, либо, в противном случае, враждуют. Известно, что среди
любых трех учащихся по крайней мере двое дружат. В классе на
собрании произошла ссора, после которой некоторые пары поссорились,
а некоторые подружились, причем так, что все равно среди любых трех
учащихся хотя бы двое дружат. Докажите, что не менее 30 пар,
друживших до ссоры, остались дружить.
Решение:
Покажем, что среди любых 6 учащихся найдутся двое оставшихся дружить
после ссоры. Если это не так, то все которые дружили стали враждовать и
наоборот. Но это невозможно, т.к. среди любых 6 найдутся либо, три попарно
дружащих, либо, три попарно враждующих. Рассмотрим теперь граф – две
вершины соединим если пара осталась дружить. Можно показать, используя
индукцию, что в таком графе на n вершинах по крайней мере
. Переход сделан.
Задача 9: В классе, в котором учатся 20 человек, каждые два либо
дружат, либо, в противном случае, враждуют. Известно, что среди
любых трех учащихся по крайней мере двое дружат. В классе на
собрании произошла ссора, после которой некоторые пары поссорились,
а некоторые подружились, причем так, что все равно среди любых трех
учащихся хотя бы двое дружат. Докажите, что не менее 30 пар,
друживших до ссоры, остались дружить.
Решение:
Покажем, что среди любых 6 учащихся найдутся двое оставшихся дружить
после ссоры. Если это не так, то все которые дружили стали враждовать и
наоборот. Но это невозможно, т.к. среди любых 6 найдутся либо, три попарно
дружащих, либо, три попарно враждующих. Рассмотрим теперь граф – две
вершины соединим если пара осталась дружить. Можно показать, используя
индукцию, что в таком графе на n вершинах по крайней мере
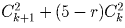 , где n = 5k + r, 0 ≤ r ≤ 4.
Задача 10: Найдите все натуральные числа a, b и c такие, что корни
уравнений x² – 2ax + b = 0, x² – 2bx + c = 0, x² – 2c + a = 0
являются натуральными числами.
, где n = 5k + r, 0 ≤ r ≤ 4.
Задача 10: Найдите все натуральные числа a, b и c такие, что корни
уравнений x² – 2ax + b = 0, x² – 2bx + c = 0, x² – 2c + a = 0
являются натуральными числами.Решение: Из условия вытекает, что a² – b, b² – c и c² – a – точные квадраты. Так как a² – b ≤ (a – 1)², то b ≥ 2a – 1. Аналогично, c ≥ 2b – 1 и a ≥ 2c – 1. Сложив последние три неравенства получим, что a + b + c ≤ 3, но тогда a = b = c = 1 и ясно, что найденные числа удовлетворяют условию задачи.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> X, 1995 >> Первый тур | Убрать решения |