Задача 1: На плоскости проведены четыре прямые так, что любые две из них
пересекаются, а никакие три не проходят черех одну точку. На каждой из
этих прямых три точки пересечения с остальными определяют два отрезка.
Могут ли восемь образовавшихся отрезков иметь длины: 1; 1; 1,5; 1,5;
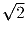
; 2; 2; 3?
Задача 2: Найдите все функции f: R → R ,
удовлетворяющие уравнению f(x²) – f(y²) = (x + y)(f(x) – f(y)) для всех x,y ∈ R .
Задача 3: В теннисном клубе n теннисистов a
1, a
2, …, a
n.
Для участия в парных состязаниях они образовали n пар K
1, K
2,
…, K
n.
Известно, что среди этих пар есть пара (a
i,a
j) тогда и только тогда,
когда в парах K
i и K
j есть один общий теннисист. Докажите, что каждый
теннисист участвует ровно в двух парах.
Задача 4: В клетках квадрата 5 × 5 расставлены целые числа. Докажите, что
найдутся две строки и два столбца, сумма чисел на пересечении которых
делится на 4.
Задача 5: Можно ли квадрат со стороной 5 расположить на координатной плоскости
так, что он покроет 21 целочисленную точку (квадрат с границей).
Задача 6: Можно ли сложить какой-нибудь прямоугольник из набора, содержащего
один трехклеточный уголок и остальные – четырехклеточные?
Задача 7: Докажите, что при n ≥ 3 для любого набора чисел
0 ≤ a
1 ≤ a
2 ≤ … ≤ a
n выполняется неравенство
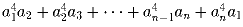
.
Задача 8:
На координатной плоскости нарисовали параболу y = (x – a)²,
где a > 0, и отметили точки A и B ее пересечения с биссектрисой
угла между координатными осями и точку C – вершину параболы. Затем все
линии и точки, кроме точек A, B, C стерли. Восстановите с помощью циркуля и
линейки точку D(1;0).
Задача 9: Докажите, что для любого натурального n можно найти натуральное m,
кратное n, сумма цифр которого равна n.
Задача 10: Малыш и Карлсон разрезали круглый торт прямолинейными разрезами,
проходящими через его центр, на 20 одинаковых кусков. Они договорились
поочередно съедать по 3 произвольных куска, а оставшиеся 2 куска
достанутся Малышу, если они окажутся рядом, и Карлсону в противном случае.
Начинает есть, конечно, Карлсон. Кто из них сумеет съесть больше кусков
торта?


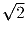 ; 2; 2; 3?
Задача 2: Найдите все функции f: R → R ,
удовлетворяющие уравнению f(x²) – f(y²) = (x + y)(f(x) – f(y)) для всех x,y ∈ R .
Задача 3: В теннисном клубе n теннисистов a1, a2, …, an.
Для участия в парных состязаниях они образовали n пар K1, K2,
…, Kn.
Известно, что среди этих пар есть пара (ai,aj) тогда и только тогда,
когда в парах Ki и Kj есть один общий теннисист. Докажите, что каждый
теннисист участвует ровно в двух парах.
Задача 4: В клетках квадрата 5 × 5 расставлены целые числа. Докажите, что
найдутся две строки и два столбца, сумма чисел на пересечении которых
делится на 4.
Задача 5: Можно ли квадрат со стороной 5 расположить на координатной плоскости
так, что он покроет 21 целочисленную точку (квадрат с границей).
Задача 6: Можно ли сложить какой-нибудь прямоугольник из набора, содержащего
один трехклеточный уголок и остальные – четырехклеточные?
Задача 7: Докажите, что при n ≥ 3 для любого набора чисел
0 ≤ a1 ≤ a2 ≤ … ≤ an выполняется неравенство
; 2; 2; 3?
Задача 2: Найдите все функции f: R → R ,
удовлетворяющие уравнению f(x²) – f(y²) = (x + y)(f(x) – f(y)) для всех x,y ∈ R .
Задача 3: В теннисном клубе n теннисистов a1, a2, …, an.
Для участия в парных состязаниях они образовали n пар K1, K2,
…, Kn.
Известно, что среди этих пар есть пара (ai,aj) тогда и только тогда,
когда в парах Ki и Kj есть один общий теннисист. Докажите, что каждый
теннисист участвует ровно в двух парах.
Задача 4: В клетках квадрата 5 × 5 расставлены целые числа. Докажите, что
найдутся две строки и два столбца, сумма чисел на пересечении которых
делится на 4.
Задача 5: Можно ли квадрат со стороной 5 расположить на координатной плоскости
так, что он покроет 21 целочисленную точку (квадрат с границей).
Задача 6: Можно ли сложить какой-нибудь прямоугольник из набора, содержащего
один трехклеточный уголок и остальные – четырехклеточные?
Задача 7: Докажите, что при n ≥ 3 для любого набора чисел
0 ≤ a1 ≤ a2 ≤ … ≤ an выполняется неравенство
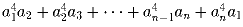 .
Задача 8:
На координатной плоскости нарисовали параболу y = (x – a)²,
где a > 0, и отметили точки A и B ее пересечения с биссектрисой
угла между координатными осями и точку C – вершину параболы. Затем все
линии и точки, кроме точек A, B, C стерли. Восстановите с помощью циркуля и
линейки точку D(1;0).
Задача 9: Докажите, что для любого натурального n можно найти натуральное m,
кратное n, сумма цифр которого равна n.
Задача 10: Малыш и Карлсон разрезали круглый торт прямолинейными разрезами,
проходящими через его центр, на 20 одинаковых кусков. Они договорились
поочередно съедать по 3 произвольных куска, а оставшиеся 2 куска
достанутся Малышу, если они окажутся рядом, и Карлсону в противном случае.
Начинает есть, конечно, Карлсон. Кто из них сумеет съесть больше кусков
торта?
.
Задача 8:
На координатной плоскости нарисовали параболу y = (x – a)²,
где a > 0, и отметили точки A и B ее пересечения с биссектрисой
угла между координатными осями и точку C – вершину параболы. Затем все
линии и точки, кроме точек A, B, C стерли. Восстановите с помощью циркуля и
линейки точку D(1;0).
Задача 9: Докажите, что для любого натурального n можно найти натуральное m,
кратное n, сумма цифр которого равна n.
Задача 10: Малыш и Карлсон разрезали круглый торт прямолинейными разрезами,
проходящими через его центр, на 20 одинаковых кусков. Они договорились
поочередно съедать по 3 произвольных куска, а оставшиеся 2 куска
достанутся Малышу, если они окажутся рядом, и Карлсону в противном случае.
Начинает есть, конечно, Карлсон. Кто из них сумеет съесть больше кусков
торта?