Задача 1:
Пусть f(x) — нечетная возрастающая функция. Докажите, что для любых чисел
a, b и c, сумма которых равна нулю, выполнено неравенство
f(a)f(b) + f(b)f(c) + f(c)f(a) ≤ 0.
Задача 2:
Сколько диагоналей можно провести в выпуклом n-угольнике так, чтобы
каждая пересекалась не более чем с одной другой? (Совпадение концов
диагоналей пересечением не считается).
Задача 3:
1997 фишек расположены на плоскости в вершинах выпуклого 1997-угольника.
За один ход можно разбить их на две группы и фишки первой группы
сдвинуть на какой-нибудь вектор, а остальные фишки оставить на месте.
Может ли случиться, что после
а) 9; б) 10 ходов все фишки окажутся на одной прямой?
Задача 4:
Четырехугольник ABCD вписан в окружность с центром O. Пусть E —
точка пересечения прямых AB и CD, F — точка пересечения прямых
AD и BC.
а) Доказать, что все шесть описанных окружностей треугольников ABF,
CDF, BEC, ADE, BOD и AOC пересекаются в некоторой
общей точке K.
б) Верно ли, что точка K лежит на прямой EF, а прямые
EF и OK перпендикулярны?
Задача 5:
Пусть f(x) — непрерывная функция, определенная на отрезке [0;5],
причем
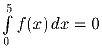
.
а) Обязательно ли существует такой отрезок [a;b] длины 2,
содержащийся в отрезке [0;5], что 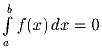 ?
?
б) Докажите, что существует отрезок [a;b] длины 2 или 3,
содержащийся в отрезке [0;5], что 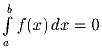 .
.
Задача 6:
Все вершины одного куба лежат на поверхности другого. Может ли так
случиться, что никакая грань первого куба не параллельна никакой
грани второго?


 .
.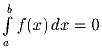 ?
?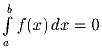 .
.